[3Blue1Brown] Chapter 1 | Vectors

{학습 목적}
Chapter 1에서는  벡터에 대한 여러가지 관점과 선형대수의 전반적인 주제를 다루는 벡터의 합과 스칼라 곱에 대해서 설명한다.
이 개념을 배우는 이유는 벡터를 공간의 화살표라는 문맥에서 숫자-리스트 라는 관점으로 이해하는 것처럼 벡터의 3가지 관점 사이로 번역해보면서 선형대수가 다양한 분야에서 어떻게 유용하게 쓰이는지 파악하기 위해서라고 생각한다. 

 

 

<벡터>

 

기본적, 근본적 선형대수의 구성조각은 벡터이다. 

 

[벡터에 대한 3가지 관점] 

- Physics: 벡터는 공간에서의 화살표

- CS: 벡터는 순차 숫자 리스트

- Mathematics: 벡터의 연산(합, 곱)이 가능하다면 무엇이든 벡터로 볼 수 있다. 

 

벡터의 합, 스칼라 곱이 선형대수 전반에 걸쳐 중요한 역할 담당!

 

 

[벡터의 합]

벡터를 하나의 움직임(특정한 방향과 거리를 가진 움직임)과 단계로 본다. 

 

 

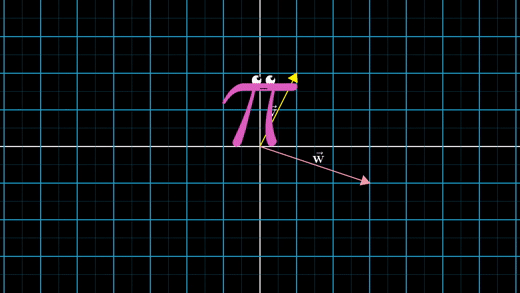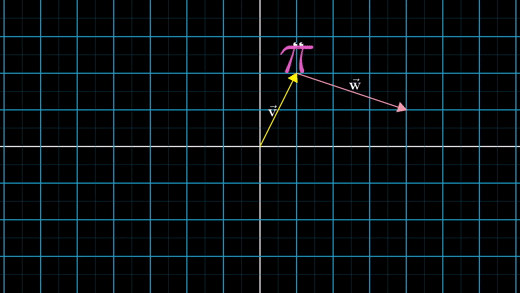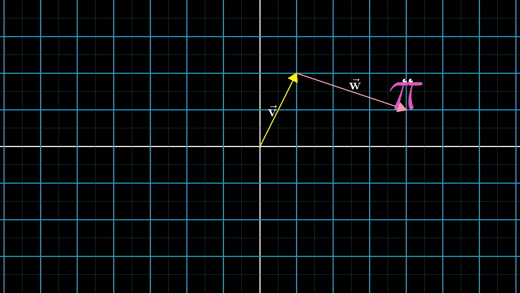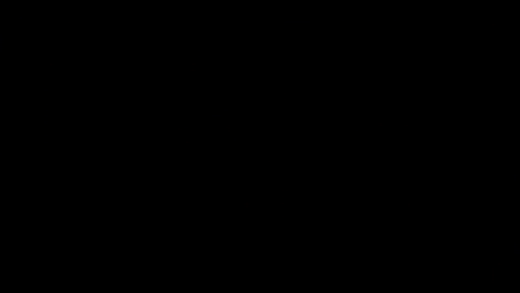
만약 첫 번째 벡터를 따라 이동하고, 다음으로 두 번째 벡터를 따라 이동한다면, 전체적인 효과는 두 벡터의 합을 따라 이동한 것과 같을 것이다. 

 

 

[벡터의 곱]

스케일링(Scaling): 벡터의 길이를 늘이거나 줄이거나, 방향을 뒤집는 것 

스칼라(Scalar): 2,1/3,-1.8과 같이 벡터 스케일링에 사용되는 숫자들 

 

숫자 리스트라는 컨셉에서, 벡터에 스칼라를 곱한다는 것은 리스트의 각 원소에 해당 스칼라(숫자)를 곱하는 것과 같다. 

 

 

• 벡터란?
  
  • 공간에서 특정한 방향과 거리를 가진 움직임이자 숫자 리스트
• 벡터의 합이란?
  • 벡터를 하나의 움직임과 단계로 보아 모든 단계를 거친 후 나오는 결과  
• 벡터의 곱이란?
  • 벡터의 길이를 늘이거나 줄이거나 방향을 뒤집는 것