K-평균 알고리즘의 이해
- 군집화의 기준이 되는 중심점을 군집화 개수만큼 설정하여 적합한 위치에 가져다 놓는다.
- 각 데이터는 가장 가까운 중심점에 소속된다.
- 소속이 결정되면 중심점이 소속된 데이터의 평균 중심으로 이동된다.
- 중심점이 이동했기 때문에 데이터들이 가까운 중심점으로 소속을 변경한다.
- 3-4과정을 반복한다.
- 데이터들의 소속변경이 없으면 군집화를 종료한다.

<k-평균의 장점>
- 일반적인 군집화에서 가장 많이 활용되는 알고리즘
- 알고리즘이 쉽고 간결하다.
<k-평균의 단점>
- 거리 기반 알고리즘으로 속성의 개수가 매우 많을 경우 군집화 정확도가 떨어진다. (이를 위해 PCA로 차원감소를 적용해야 할 수도 있다.)
- 반복을 수행하는데, 반복 횟수가 많을 경우 수행 시간이 매우 느려진다.
- 몇 개의 군집(cluster)을 선택해야 할지 가이드하기가 어렵다.
사이킷런 KMeans 클래스
class sklearn.cluster.Kmeans (n_cluster=8, init='k_means++', n_init=10, max_iter=300,...)- KMeans 초기화 파라미터 중 가장 중요한 파라미터는 n_cluster, 군집화 개수 , 즉 군집 중심점의 개수를 의미
- init는 초기에 군집 중심점의 좌표를 설정할 방식을 말하며, 보통은 임의로 중심을 설정하지 않고 k-means++ 방식으로 최초 설정
- max_iter는 최대 반복 횟수이며, 이 횟수 이전에 모든 데이터 중심점 이동이 없으면 종료
- Kmeans 알고리즘은 fit()/ fit_transform() 메서드를 이용해 수행
- Kmeans 객체는 군집화 수행이 완료돼 군집화와 관련된 주요 속성을 알 수 있음
- labels_ : 각 데이터 포인트가 속한 군집 중심의 레이블
- cluster_centers_: 각 군집 중심점 좌표(Shape 는 [군집개수, 피처개수]). 이를 이용하면 군집 중심점의 좌표가 어디인지 시각화 할 수 있음
K-평균을 이용한 붓꽃 데이터 세트 군집화
- 꽃받침, 꽃잎의 길이(붓꽃데이터 피처 4개 중 2개 선택 )에 따라 각 데이터의 군집화가 어떻게 이루어지는지 확인하고, 레이블 값과 비교
- n_cluster=3, init=k-means++, max_iter=300
- 군집화 수행 후 반환된 kmeans 객체의 labels_ 속성값 확인
- 실제 분류 레이블 값과 비교를 위해 target 칼럼, cluster 칼럼 지정하여 group by 연산을 통해 각각의 값 개수를 비교
- Target 0 : 1번 군집으로 잘 분류
- Target 1 : 0번 군집 48개, 2번 군집 2개
- Target 2 : 0번 군집 14개, 2번 군집 36개
- 2차원 평면상에서 군집화를 시각화 → 붓꽃 데이터 피처값이 4개이므로 PCA를 이용해 2개의 피처값으로 차원 축소
- pca_x, pca_y 로 X좌표, Y 좌표 표현
- 각 군집별로 cluster 0 은 마커 ‘o’, cluster 1은 마커 ‘s’, cluster 2는 마커 ‘^’로 표현
#k-평균을 이용한 붓꽃 데이터 세트 군집화
from sklearn.preprocessing import scale
from sklearn.datasets import load_iris
from sklearn.cluster import KMeans
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
%matplotlib inline
iris = load_iris()
#더 편리한 데이터 핸들링을 위한 DataFrame 변환
irisDF = pd.DataFrame(data=iris.data, columns =['sepal_length','sepal_width', 'petal_length','petal_width'])
irisDF
#붓꽃 데이터 세트를 3개의 그룹으로 군집화
kmeans = KMeans(n_clusters=3, init='k-means++', max_iter=300, random_state=0)
kmeans.fit(irisDF)
print(kmeans.labels_)
#groupby 연산을 통해 실제 분류값인 target label 값과 cluster 값 비교
irisDF['target'] = iris.target
irisDF['cluster'] = kmeans.labels_
iris_result =irisDF.groupby(['target', 'cluster'])['sepal_length'].count()
print(iris_result)
[output]
[1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1 1 1 1 1 1 0 0 2 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 2 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 2 0 2 2 2 2 0 2 2 2 2
2 2 0 0 2 2 2 2 0 2 0 2 0 2 2 0 0 2 2 2 2 2 0 2 2 2 2 0 2 2 2 0 2 2 2 0 2
2 0]
target cluster
0 1 50
1 0 48
2 2
2 0 14
2 36
Name: sepal_length, dtype: int64# 시각화를 위해 4개의 피처 -> 2개의 피처로 차원 축소
from sklearn.decomposition import PCA
pca=PCA(n_components=2)
pca_transformed = pca.fit_transform(iris.data)
irisDF['pca_x'] = pca_transformed[:,0]
irisDF['pca_y'] = pca_transformed[:,1]
irisDF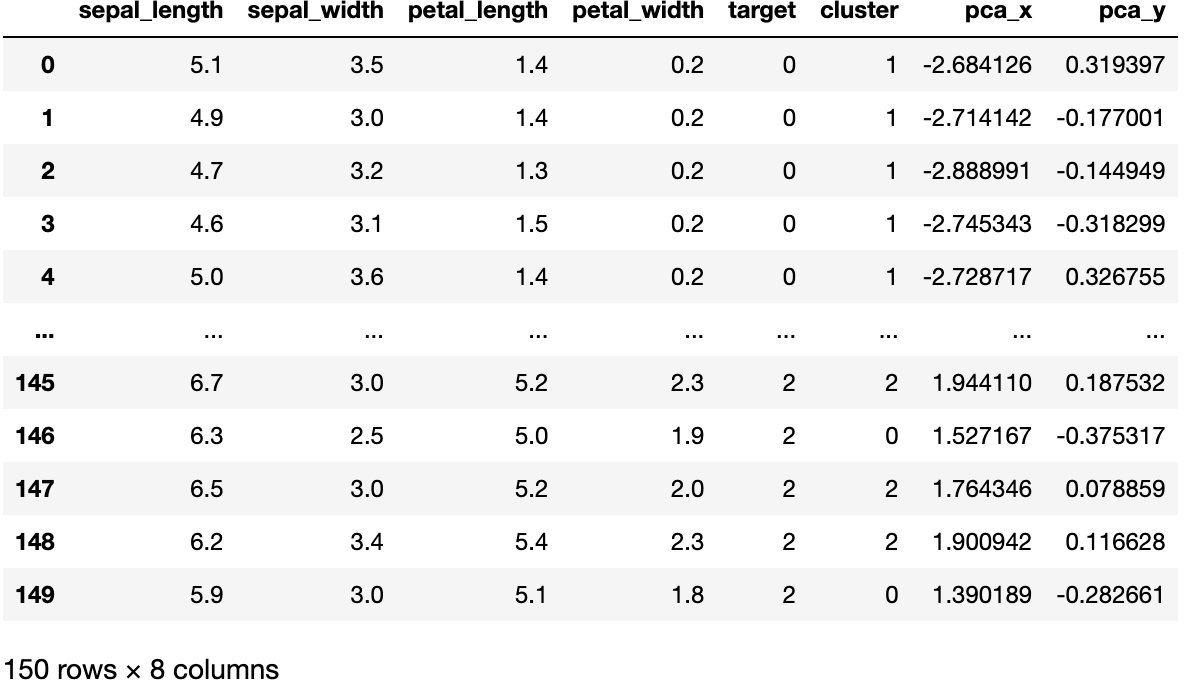
# 군집 값이 0,1,2 인 경우마다 별도의 인덱스 추출
marker0_ind = irisDF[irisDF['cluster']==0].index
marker1_ind = irisDF[irisDF['cluster']==1].index
marker2_ind = irisDF[irisDF['cluster']==2].index
#군집 값 0,1,2에 해당하는 인덱스로 각 군집 레벨의 pca_x, pca_y 값 추출. o,s,^ 마커로 표시
plt.scatter(x=irisDF.loc[marker0_ind, 'pca_x'], y=irisDF.loc[marker0_ind, 'pca_y'], marker='o')
plt.scatter(x=irisDF.loc[marker1_ind, 'pca_x'], y=irisDF.loc[marker1_ind, 'pca_y'], marker='s')
plt.scatter(x=irisDF.loc[marker2_ind, 'pca_x'], y=irisDF.loc[marker2_ind, 'pca_y'], marker='^')
plt.xlabel('PCA 1')
plt.ylabel('PCA 2')
plt.title('3 Cluster Visualization by 2 PCA Components')
plt.show()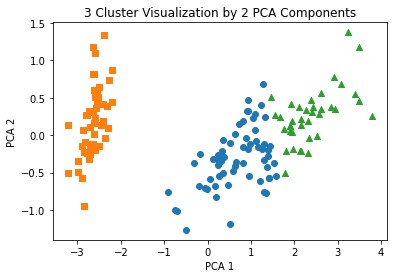
군집화 알고리즘 테스트를 위한 데이터 생성
X,y = make_blobs(n_samples=100, n_features= , centers= , cluster_std= , ..)- make_blobs() API
- 하나의 클래스에 여러개의 군집이 분포하는 분류 태스트용 데이터를 생성
- make_blobs() :개별 군집의 중심점과 표준편차 제어기능 추가됨
- n_samples : 생성할 데이터의 총 개수
- n_features : 데이터의 피처 개수
- centers: init 값, 군집의 개수, ndarray 로 표현하면 개별 중심점의 좌표를 의미
- cluster_std: 생성될 군집데이터의 표준편차
#군집화 알고리즘 테스트를 위한 데이터 생성 : make_blobs()
import numpy as np
import matplotlib.pyplot as plt
from sklearn.cluster import KMeans
from sklearn.datasets import make_blobs
%matplotlib inline
X,y = make_blobs(n_samples=200, n_features=2, centers=3, cluster_std=0.8, random_state=0)
print(X.shape, y.shape)
#y target 값의 분포를 확인
unique, counts = np.unique(y, return_counts = True)
print(unique, counts)
[output]
(200, 2) (200,)
[0 1 2] [67 67 66]- np.unique( array, return_counts = False)
- 배열(array) 의 고유한 요소를 반환
- return_counts = True로 지정할 경우 각 고유 항목이 array 에 나타나는 횟수도 반환
# 데이터 가공을 편리하게 하기 위해 DataFrame 생성
import pandas as pd
clusterDF = pd.DataFrame(data=X, columns=['ftr1', 'ftr2'])
clusterDF['target'] = y
clusterDF
# make_blob()으로 만든 피처 데이터 세트가 어떤 군집화 분포를 가지고 있는지 확인
target_list = np.unique(y)
#각 타겟별 산점도의 마커 값
markers=['o', 's', '^','P', 'D', 'H', 'x']
#3개의 군집 영역으로 구분한 데이터 세트를 생성했으므로 target_list 는 [0,1,2]
#target==0, target==1, target==2 로 scatter plot 을 marker별로 생성
for target in target_list:
target_cluster = clusterDF[clusterDF['target']==target]
plt.scatter(x=target_cluster['ftr1'], y=target_cluster['ftr2'], edgecolor='k',
marker=markers[target])
plt.show()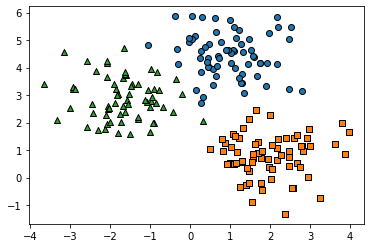
#KMeans 객체를 이용해 X 데이터를 K-Means 클러스터링 수행
kmeans = KMeans(n_clusters=3, init='k-means++', max_iter=200, random_state=0)
cluster_labels = kmeans.fit_predict(X)
clusterDF['kmeans_label'] = cluster_labels
#cluster_centers_는 개별 클러스터의 중심 위치 좌표 시각화를 위해 추출
centers = kmeans.cluster_centers_
unique_labels = np.unique(cluster_labels)
markers = ['o', 's', '^', 'P', 'D', 'H', 'x']
#군집된 label 유형별로 iteration 하면서 marker 별로 scatter plot 수행
for label in unique_labels:
label_cluster = clusterDF[clusterDF['kmeans_label']==label]
center_x_y = centers[label]
plt.scatter(x=label_cluster['ftr1'], y=label_cluster['ftr2'], edgecolor='k',
marker=markers[label])
#군집 중심별 위치 좌표 시각화
plt.scatter(x=center_x_y[0], y=center_x_y[1], s=200, color='white',
alpha=0.9, edgecolor='k', marker=markers[label])
plt.scatter(x=center_x_y[0], y=center_x_y[1], s=70, color='k', edgecolor='k',
marker='$%d$' % label)
plt.show()
print(clusterDF.groupby('target')['kmeans_label'].value_counts())
[output]
target kmeans_label
0 0 66
1 1
1 2 67
2 1 65
2 1
Name: kmeans_label, dtype: int64Target 0 이 cluster label 0, Target 1이 label 2, Target 2가 label 2로 거의 대부분 잘 매핑된 것을 확인할 수 있음
Ref) 파이썬 머신러닝 완벽가이드
'데이터 > 머신러닝' 카테고리의 다른 글
| [Clustering] Chapter 7 | 군집화 실습 - 고객 세그멘테이션 (1) | 2023.01.28 |
|---|---|
| [Clustering] Chapter 7 | 군집화 (02. 군집 평가) (0) | 2023.01.23 |
| [Classification] Chapter 4 | 분류(01. 분류의 개요~02. 결정 트리) (0) | 2022.09.05 |
| [Evaluation] Chapter 3 | 평가 (06. 피마 인디언 당뇨병 예측) (0) | 2022.08.29 |
| [Evaluation] Chapter 3 | 평가 (04. F1 스코어 ~ 05. ROC 곡선과 AUC) (0) | 2022.08.29 |
