목차
8.1 Confidence Intervals
8.2 Hypothesis Testing
8장에서는 Confidence Intervals(t-intervals)와 Hypothesis testing(t-test)을 통한 Population means의 추론을 배운다.
8.1 Confidence Intervals
Confidence Intervals(신뢰구간)
- 정의 : 우리가 추정하고자 하는 µ에 대한 신뢰구간이란 µ의 "plausible(타당한, 그럴듯한)" 값을 포함하는 구간이다.
EX) 강의에 참석한 60명의 키를 수집한다고 해보자

평균 키에 대한 구간으로 어떤 것이 더 plausible 해보이는가? 2번!

즉, 신뢰구간은 범위+타당성을 정의하는 구간이다.
- 어떻게? : 신뢰 구간은 점 추정치와 표준 오차를 이용하게 결정하게 된다.
왜 ? 표준오차는 sampling distribution(표본 분포, 샘플 평균들의 분포)의 표준 편차이기 때문에 점 추정치(샘플 평균)를 기준으로 구간을 정할 수 있게 된다.
말이 어렵기 때문에 표준오차의 정의에서부터 다시 복기해본다!
❓ <표준오차(standard error)란?>
표본 평균의 표준 편차

표준 편차 = 편차의 제곱의 평균에 루트를 씌운 값
편차 = 변량 - 평균
즉, 표준 편차는 변량들이 평균에서 얼마나 떨어져 있는지를 나타내주는 값이다.
표준 오차는 표본 평균(추정값)의 표준 편차이다
그러니까,, 이 때 구하는 편차에서의 변량은 표본 평균이 된다!
그리고 편차에서의 평균은 모평균(참값)이 된다.
따라서 표준 오차를 구할 때 ⭐️ 편차(오차)는 표본 평균 - 모평균(추정값-참값) ⭐️을 의미하게 된다.
그리고 이 편차를 오차라고 부른다.

🙋♀️ !! 즉, 표준 오차가 각각의 표본 평균(점 추정값)이 모평균(참값)에서 얼마나 떨어져있는지를 나타내주기 때문에 우리가 알고자하는 µ의 값의 범위들을 알려주게 되는 것이다!

- 신뢰구간을 정의 할 때는 Confidence level(신뢰도) 도 함께 정의되어야한다.
EX) µ가 90%의 확률로 해당 구간 안에 들어있다.
즉, Confidence level(신뢰도)이란 우리가 추정하고자 하는 µ가 신뢰 구간 안에 있는 확률을 의미한다.
- typical confidence level = 90%, 95%, 99%
- 1 - 𝛼 의 형태로 나타냄 (𝛼 = 0.1, 0.05, 0.01)
t-Intervals
가장 기본적인 신뢰구간은 t-분포를 사용하여 계산하기 때문에 신뢰구간을 t-구간이라고도 한다.
- 신뢰구간을 구하려면 ⭐️1. 표본 평균 분포가 정규 분포를 따르거나 2. 표본 크기가 30 이상⭐️이어야 한다.(CLT 정리에 따라서)
- ⭐️ 하지만 두 조건 다 만족하지 않아도, t -분포를 통해 어느 정도 신뢰구간을 계산할 수 있다.
❓ <CLT 란?>


t-분포를 이해하기 전에 카이제곱, 자유도에 대한 정의를 살펴보자면,, 😰
❓ <카이제곱분포와 자유도>


❓ <t-분포란?>
t 분포는 정규분포, 카이제곱 분포로부터 정의된다.
확률변수 X가 표준 정규분포 N(0,1)을 따르고, 확률변수 Y가 자유도 v인 카이제곱 분포를 따르면서, X와 Y가
자유도를 가진 t -분포는 다음과 같이 정의된다.


🧐 t-분포는 언제 쓰이는 걸까?
t분포는 모집단이 정규분포를 하더라도 분산 σ²이 알려져 있지 않고 표본의 수가 적은 경우에, 평균 μ에 대한 신뢰구간 추정 및 가설검정에 아주 유용하게 쓰이는 분포이다.
이게 그러니까,, t분포의 확률변수 T를 정의할 때 표준정규분포를 따르는 확률 변수가 들어있다.
즉, 이를 찾기 위해서는 모집단의 분산을 알아야하는데 모분산은 전수조사를 해야 구할 수 있기 때문에 현실적으로 구할 수 없다.
따라서 자유도에 따라 달라지는 t 분포를 사용함으로써 표본 분산으로 모분산을 근사화 한 값을 사용하게 되는 것!
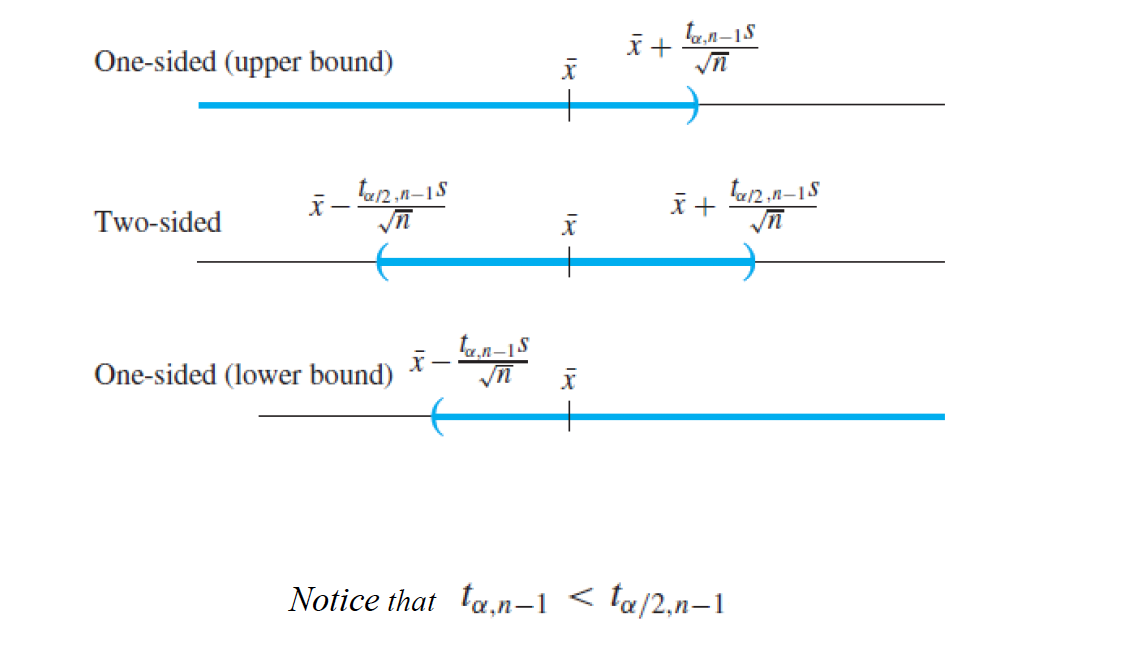
Two-sided t-interval
- 신뢰도(1 - 𝛼) 에 따른 신뢰구간의 계산

- t 분포는 자유도를 기준으로 t 분포표에서 C.P(critical point)에 해당하는 평균 μ의 추정 확률을 구하게 된다.

- t 구간은 점 추정치(sample mean)를 기준으로 c.p x s.e(standard error) 만큼 좌우 동일한 범위로 구간이 정의된다.

Length of t-intervals
- 신뢰구간(t-구간)의 길이

해석 1) s.e가 줄어들면 point estimate(점 추정치,우리가 추정한 평균)가 모평균에 가까워질 확률이 높아짐 -> 신뢰 구간 감소
해석 2) 신뢰도(1 - 𝛼) 가 커질수록 (= 𝛼이 작아질수록 = t 분포 확률이 작아진다는 것) 모평균에 가까워질 확률이 낮아짐 -> 신뢰 구간 증가
ex) 신뢰도 10%로 구간 안에 들어있다면 신뢰구간이 짧아도 되지만 99%의 확률로 들어있다고하면 구간이 더 길어야한다고 생각하면 이해하기 쉽다!
📝 예제 )
milk container 부피(L)에 대한 통계량을 보고 신뢰도 95%인 milk container 부피에 대한 평균의 신뢰구간을 구하여라

💡 풀이 )

⚠️ 주의할 점
데이터 하나가 아니라 우리가 추정한 평균이 해당 신뢰구간 안에 들어있을 확률이 95%라는 것이다!
따라서 모든 데이터가 이 구간 안에 들어있다고 해석하면 안됨🙅♀️
Effect of sample size
- sample 사이즈가 증가 -> 신뢰구간 감소
sample 사이즈가 클수록 모집단에 가까워지게 되므로 추정값의 신뢰도는 더 올라감 따라서 신뢰구간 감소!

sample 사이즈가 클수록 모집단에 가까워지게 되므로 추정값의 신뢰도는 더 올라가기 때문에 신뢰구간이 감소한다고 이해하면 쉽다.
🤷♀️ : 앞에서 신뢰도(1 - 𝛼)가 증가하면 critical point가 증가하기 때문에 신뢰구간이 길어진다고했는데??
🤓 : critical point 도 sample size(n)의 영향을 받긴하지만 sample size가 특히 더 커지면 c.p의 영향력이 작아져서 (왜?)
L과 n의 관계를 우선적으로 고려하게 된다.
- 신뢰 구간의 최대 길이를 L0로 가져간다고 가정하면 n(sample size)의 값은 다음과 같이 구할 수 있다.

🤷♀️ : 하지만, c.p를 구할 때도 n값이 필요한데 이를 어떻게 계산할 수 있을까?
- 🤓 : n이 커질수록 c.p의 값은 작아지는 경향이 있기 때문에,
만약 sample size가 n1이고 L0를 만족하기 위한 sample size가 몇 개 더 필요한지 구하는 상황이라면, c.p를 구할 때 n1을 대입해서 사용한다.

📝 예제 )
현재 대학생들의 평균 신장에 대한 통계는 다음과 같다.
Initial sample size : 20
Sample standard deviation : 9
Confidence : 99% (𝛼 = 0.01)
최대 신뢰 구간 길이 4cm로 원한다고 했을 때, 더 요구되어지는 sample size는 몇인가?
💡 풀이)

One-sided t-Intervals
- population mean이 적어도 ~ 이상일 것이다. or 적어도 ~이하일 것이다. 라고 단측 구간을 주는 것
- upper bound :
자유도가 n-1인 t 분포를 따르는 랜덤 변수가 있을 때(우리는 μ를 모르는 상황), μ가 c.p보다 클 확률은 1 - 𝛼이다.
따라서 μ에 대한 upper bound를 주는 단측 신뢰구간을 정의할 수 있게된다.

- lower bound:

- two-sided와 비교했을때, one side의 c.p들이 좀 더 작은 경향이 있다.
📝 예제 )
방사성 연구실에서 일하는 worker들은 자신이 방사선에 노출되었는지 알고싶어한다.
수집된 28(n)개의 데이터의 통계는 다음과 같다
x̄(sample mean) = 5.145
s(sample standard deviation) = 0.7524
critical point = 2.473
confidence level = 99% (𝛼 = 0.01)
실제 모집단의 노출 평균의 단측 신뢰구간에 대해서 구해보자.
💡 풀이 )

즉, 노출 수준의 평균은 99% 확률로 5.5보다 작다.
8.2 Hypothesis Test
- 특정 가설이 맞을 확률을 통계적으로 계산해서 그것을 바탕으로 의사결정을 하는 것
- 가설 검정을 위해선 2가지 statments가 필요
- (1) Null hypothesis(H0, 귀무가설)
- (2) Alternative hypothesis (HA, 대립가설)
- EX) µ= 20이라고 하는 것이 타당한가?
- 귀무가설(H0) : µ = 20
- 대립가설(HA) : µ ≠ 20
귀무가설이 맞을 가능성이 존재하면 귀무가설 채택(accpet)
충분한 근거가 보이지 않는다면 기각(recject) -> 대립가설이 맞다는 결론에 이르게 된다.
귀무가설, 대립가설에 대해 좀 더 자세히 알아보자
❓ <귀무가설>
정의 : 모집단의 특성에 대해 옳다고 제안하는 잠정적인 주장
"모집단의 모수(모집단을 조사하여 얻을 수 있는 모든 통계치)는 OO (표본의 통계치) 와 같다."
"모집단의 모수는 OO와 차이가 없다."
ex) 전국 20세 이상의 평균 키가 170cm라는 주장을 통계적으로 검정한다면, 이에 대한 귀무가설은
"20세 이상의 성인 남자(표본)의 평균 키는 170cm와 같다."가 된다.
즉, 🔅"~와 차이가 없다. " "~의 효과는 없다.", "~와 같다."🔅 라는 형식이 귀무가설이 된다.
❓ <대립가설>
정의 : 귀무가설이 거짓이라면 대안적으로 참이 되는 가설, 귀무가설이 기각됐을 때 대안적으로 채택되는 가설
"모집단의 모수는 OO 와 다르다."
"모집단의 모수는 OO와 차이가 있다."
ex) 전국 20세 이상의 평균 키가 170cm라는 주장에 대한 대립가설은 "20세 이상의 성인 남자의 평균 키는 170cm와 다르다."
즉 대립가설은 🔅"~와 차이가 있다." "~의 효과는 있다." "~와 다르다."🔅라는 형식으로 이루어진다.
- 귀무가설은 등호(=, two-sided set of hypothesis) 뿐만아니라 부등호(≥, ≤,one-sided set of hypothesis)도 사용할 수 있다. (>,< 는 사용 불가)
📝 예제 ) 자동차 제조업체는 고속도로에서 자동차의 연비가 최소 35이상이라고 주장한다. 소비자들은 고속도로를 달리는 조건에서 무작위로 자동차를 선택하고 연료효율을 측정하여 자동차 제조업체의 주장이 맞지 테스트하고자한다.
💡 풀이 ) 가설검정에서는 대안적으로 채택하고자 하는 것을 대립가설에 둔다!
귀무가설 : µ ≥ 35 -> 절대적인 참이라고 입증할 수 없음.
대립가설 : µ < 35 -> 절대적인 참이라고 입증할 수 있음. 따라서 귀무가설이 아니라는 근거를 제공해주는 역할
p-Value (유의수준)
- p-value는 데이터 셋에 기반한 귀무가설의 타당성에 대한 확률이다.
즉, 관찰된 유의수준(0< p <1) - 즉, p-value가 작을수록 귀무가설의 타당성이 낮다. (귀무가설이 기각될 확률이 높다. )
- p-value 해석
- p ≤ 0.01 : 귀무가설이 타당하지 않다 -> 귀무가설 기각, 대립가설 채택 (강한 결론)
- 0.01 < p < 0.1 : Intermediate area, 결론을 내리기 애매함 (inconclusive)
- p > 0.1 : 귀무가설이 타당하다(틀렸다고 할 수 없다). (입증된 것이 아님, 타당하지 않다는 근거가 없는 것) -> 귀무가설 채택 (약한 결론)
- one-sided set of hypothesis problem에서는 귀무가설과 대립가설을 어떻게 설정할까?
- 귀무가설을 참이라고 입증할 수는 없다! 즉, 귀무가설이 거짓이라고만 입증할 수 있는것
- 따라서 참이라고 보이고 싶은 가설을 대립가설로 두고 귀무가설을 기각하려는 증거로서 가설검증을 진행하게 됨
📝 예제 ) "이 교실에 있는 학생들은 하루에 적어도 두잔 이상의 커피를 마실 것이다." 라는 주장에 대해서 틀렸다는 것을 입증하고 싶다면
귀무가설과 대립가설을 어떻게 둬야할까?
💡 풀이 )
귀무가설 : 이 교실에 있는 학생들은 하루에 적어도 두잔 이상의 커피를 마실 것이다. (µ ≥2)
대립가설 : 이 교실에 있는 학생들은 하루에 적어도 두잔 미만의 커피를 마실 것이다. (µ <2)
p < 0.01이라면 대립가설이 참이라는 강한 결론을 내리게 될 수 있다. (귀무가설 기각)
Interpretation of p-value
- 귀무가설이 맞다는 가정 하에서 현재 data sample 보다 훨씬 안 좋은 데이터가 발생할 확률
- 안 좋은 데이터란, 귀무가설과 동떨어진 데이터를 의미함
p-value가 작을 때와 클 때 해석하는 것이 이해가 안 돼서 교수님 강의 다시 들으면서 필기.. 🤓

Caculation of p-value
- H0 : µ = µ0, HA : µ ≠ µ0 인 two-sided hypothesis test 가 있다면 데이터 세트와 귀무가설의 불일치 확률은 t-통계를 통해 측정된다.
- ˉx = µ0 일 때, t =0
- |t|가 증가할수록 불일치가 증가

t -statistics는 n-1의 자유도 분포를 갖는 t 분포의 관측치이다.
즉, p-value는 t-statistics을 통해 다음과 같은 식으로 계산할 수 있다.
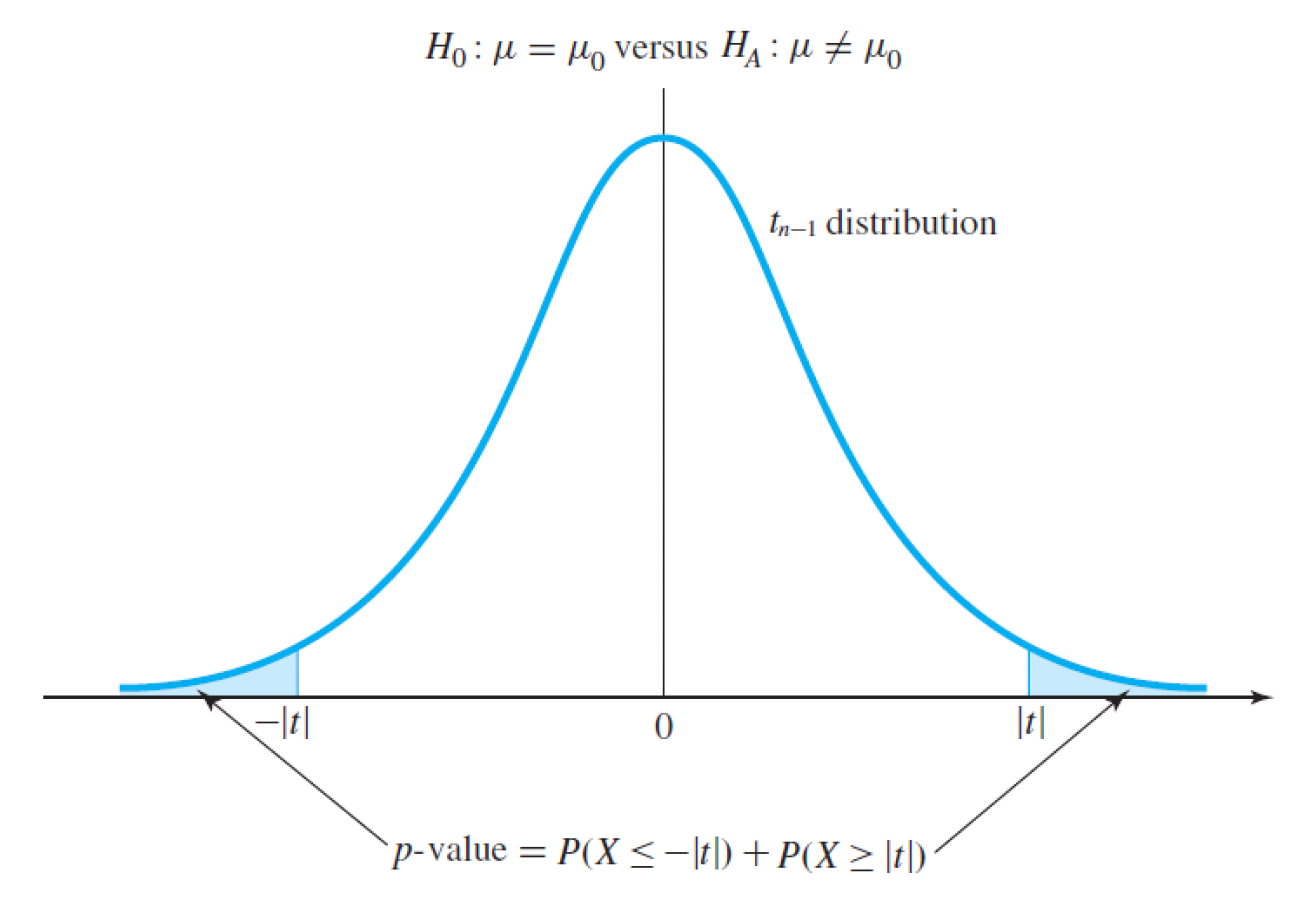
Two-sided T-test
📝 예제 ) 다음과 같은 가설이 있다.
H0 : µ = 10.0
HA : µ ≠ 10.0
그리고 sample dataset의 통계량은 다음과 같다.
n = 15, ˉx =10.6, s =1.61
이를 대입하면 t-통계량을 구할 수 있다.

따라서 p-value는 자유도 14인 t 분포를 따르는 확률 변수가 1.44보다 클 확률, 작을 확률을 더한 값이 된다.

엑셀 함수를 통해 계산하였더니 p-value는 0.172가 나왔다.

따라서 p> 0.1이기 때문에 귀무가설을 reject하지 못해 accpet 한다. (만약 µ0=10.1이라도 이 가설을 채택하게 될 것이다! )
one-sided T-test
- one-sided일 때는 worst 데이터를 어떻게 정의할까?
- H0 : µ ≤ µ0 vs HA : µ ≥ µ0 일 때
항상 worse data가 오른쪽에 존재하는 경우에 대해서 찾기 때문에 절댓값이 아닌 t를 계산하여 t 분포의 확률 변수보다 큰 부분만 p-value로 계산하면 된다.
- H0 : µ ≤ µ0 vs HA : µ ≥ µ0 일 때

- H0 : µ ≥ µ0 vs HA : µ ≤ µ0 일 때
반대로 t 분포의 왼쪽 범위에 대해서만 계산해주면 된다.

