문제 링크 : https://www.acmicpc.net/problem/1904
난이도 : 실버 3
1904번: 01타일
지원이에게 2진 수열을 가르쳐 주기 위해, 지원이 아버지는 그에게 타일들을 선물해주셨다. 그리고 이 각각의 타일들은 0 또는 1이 쓰여 있는 낱장의 타일들이다. 어느 날 짓궂은 동주가 지원이
www.acmicpc.net
문제
지원이에게 2진 수열을 가르쳐 주기 위해, 지원이 아버지는 그에게 타일들을 선물해주셨다. 그리고 이 각각의 타일들은 0 또는 1이 쓰여 있는 낱장의 타일들이다.
어느 날 짓궂은 동주가 지원이의 공부를 방해하기 위해 0이 쓰여진 낱장의 타일들을 붙여서 한 쌍으로 이루어진 00 타일들을 만들었다. 결국 현재 1 하나만으로 이루어진 타일 또는 0타일을 두 개 붙인 한 쌍의 00타일들만이 남게 되었다.
그러므로 지원이는 타일로 더 이상 크기가 N인 모든 2진 수열을 만들 수 없게 되었다. 예를 들어, N=1일 때 1만 만들 수 있고, N=2일 때는 00, 11을 만들 수 있다. (01, 10은 만들 수 없게 되었다.) 또한 N=4일 때는 0011, 0000, 1001, 1100, 1111 등 총 5개의 2진 수열을 만들 수 있다.
우리의 목표는 N이 주어졌을 때 지원이가 만들 수 있는 모든 가짓수를 세는 것이다. 단 타일들은 무한히 많은 것으로 가정하자.
입력
첫 번째 줄에 자연수 N이 주어진다. (1 ≤ N ≤ 1,000,000)
출력
첫 번째 줄에 지원이가 만들 수 있는 길이가 N인 모든 2진 수열의 개수를 15746으로 나눈 나머지를 출력한다.
📌 풀이 접근 방법
이 문제는 DP 의 대표적인 유형이라고 볼 수 있다.
나동빈님 이코테 책에 나온 <바닥공사> 문제와 유사했다!!
타일을 채울 수 있는 2진 수열의 길이인 N의 범위는 매우 크므로 만약, 이 문제를 모든 가능한 경우의 수에 대해 탐색하게 된다면 시간초과가 발생할 것이다.
예제에서의 n = 4일 때의 경우를 보면, 0011, 0000 경우에서 앞의 두 자리가 00 인 결과를 반복해서 사용하는 것을 확인할 수 있다.
이렇게 중복되는 연산의 경우가 있을 때 이를 매번 새로운 경우의 수로 처리해준다면, 쓸데없는 연산을 하게 되는 것!
따라서 최대한 효율적인 알고리즘 작성을 위해서 나온 기법이 DP(다이나믹 프로그래밍) 이다.
DP를 고려할 수 있는 조건이 2가지가있다.
1. 큰 문제를 작은 문제로 나눌 수 있어야함
2. 작은 문제에서 구한 정답은 그것을 구한 큰 문제에서도 동일
이 문제는 수열의 왼쪽에서부터 N번째까지 가능한 타일로 채워나간다고 생각한다면,
하나씩 채워나가는 과정에서 작은 문제로 쪼개어 볼 수 있다.
그리고 하나씩 채운 결과는 전체적인 결과에 포함되기 때문에 2번 조건도 만족!
그렇다면 점화식을 어떻게 세워야할까?
DP 문제 유형을 풀다보면, 역방향으로 접근하는 스킬?을 많이쓰는 것 같다. (전에 풀었떤 퇴사 문제도!!)
이 문제도 뒤에서부터 채워나간다고 생각해보았다.
1) 왼쪽부터 N-1번까지 수열이 이미 채워진 경우
마지막 타일로 올 수 있는 타일의 종류는 <1> 밖에 없기 때문에 경우의 수는 1이다.
2) 왼쪽부터 N-2번까지 수열이 이미 채워진 경우
마지막 타일로 올 수 있는 타일의 종류는 <11>, <00>이다.
하지만 <11> 의 경우 1번 경우에 포함되기 때문에 고려하지 않아도 된다. 즉, 가능한 경우의 수는 1가지!
N-3번까지 수열이 채워진 경우는 고려하지 않아도된다.
마찬가지로, 올 수 있는 타일의 종류는 <001> , <100>인데 모두 1,2번 경우에 포함된다.
그림을 그려보면, 중복되는 연산이 발생한다는 것을 확실히 이해할 수 있다.
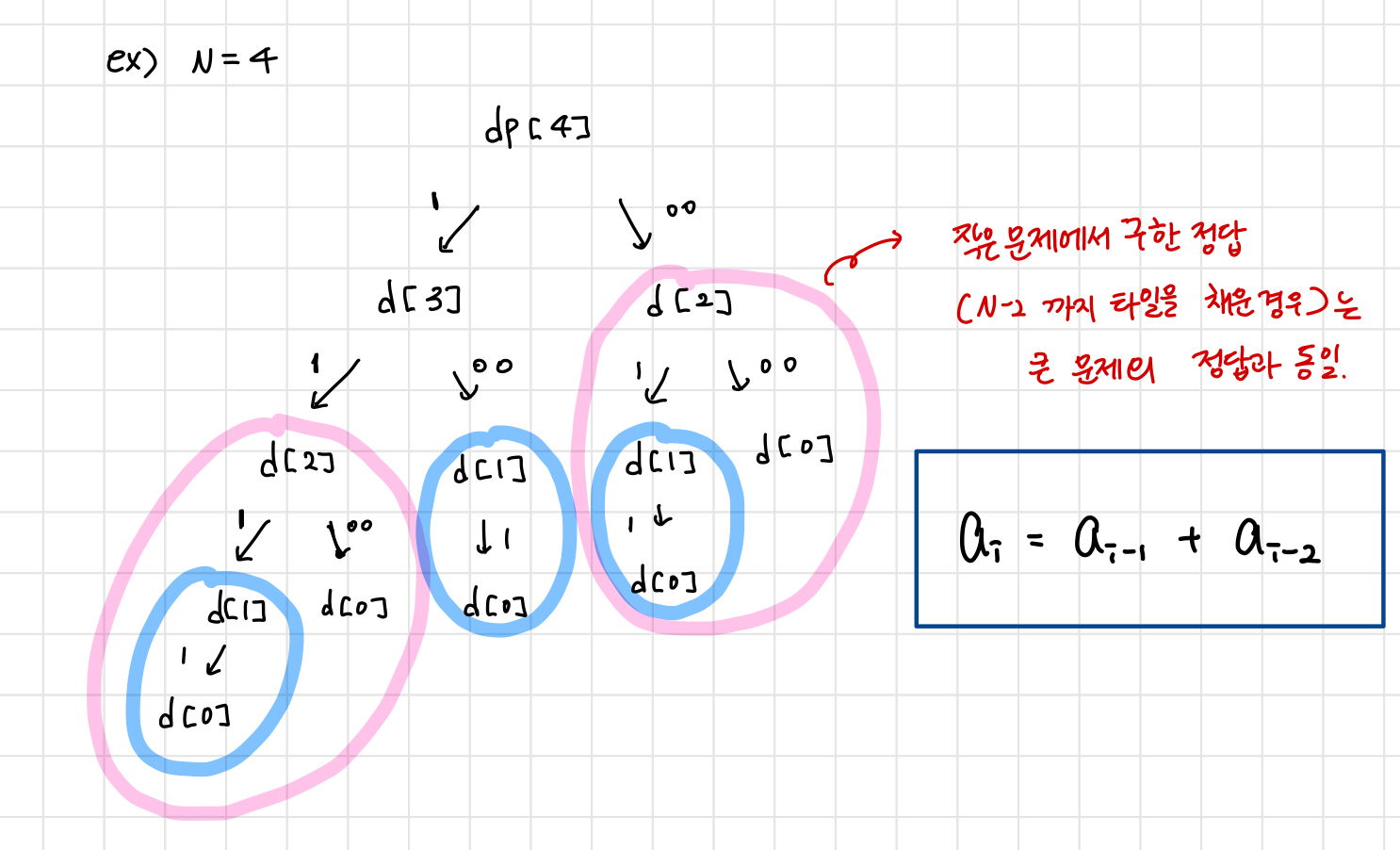
따라서 점화식은 다음과 같이 쓸 수 있다.
a_i = a_i-1 + a_i-2
..!!! 오옹 피보나치 수열과 같은 공식이 나온다.
따라서, 이 문제의 시간복잡도는 전에 계산되었던 결과를 다음계산에 그대로 가져다 활용하게 되는 것이므로
O(N)의 시간이 걸리게 된다!
📌 나의 풀이
보텀업 방식으로 코드를 작성했다.
n = int(input())
dp = [0] * 10000001
# 1칸을 채우는 경우의 수 1개, 2칸 채우는 경우의 수 2개
dp[1] = 1
dp[2] = 2
# 보텀업 dp
for i in range (3, n+1) :
dp[i] = (dp[i-1] + dp[i-2]) % 15746
print(dp[n])
오랜만에 dp문제를 풀었는데 개념 복습하게 돼서 굳굳
쉬운 문제부터 다시 차근차근 연습해야겠당
'알고리즘' 카테고리의 다른 글
| [삼성 SW 역량 테스트 기출] 백준 14888번 연산자 끼워넣기(Python) (1) | 2024.01.30 |
|---|---|
| [삼성 SW 역량테스트 기출] 백준 14500번 테트로미노(Python) (1) | 2024.01.29 |
| [백준 1759번] 암호 만들기(Python) (1) | 2024.01.27 |
| [백준 9019번] DSLR(Python) (0) | 2024.01.26 |
| [백준 15650번] N과 M(2) (1) | 2024.01.25 |
