[파이썬으로 하는 마케팅 연구와 분석] Chapter 4 | 연속변수 간의 관계

4.1 소매데이터

4.1.1 데이터 시뮬레이션

• 다채널 소매업체의 1,000명 고객에 대한 데이터셋 생성

4.1.2 온라인 및 내점 판매 데이터 시뮬레이션

• 온라인 방문과 거래에 대한 각 고객의 1년 총액 + 총 지출액
• 음이항 분포로 방문 수 
• 각 온라인 방문마다 주문확률 30% 가정하고 online_trans 변수 생성
• 로그 정규 분포 변수로 매장 내 판매 데이터 생성 

4.1.3 만족도 조사 응답 시뮬레이션

설문 조사 항목에 대해 전반적으로 관찰되지 않은 만족도(halo)와 서비스 및 제품 선택에 대한 특정 만족도 수준 기반

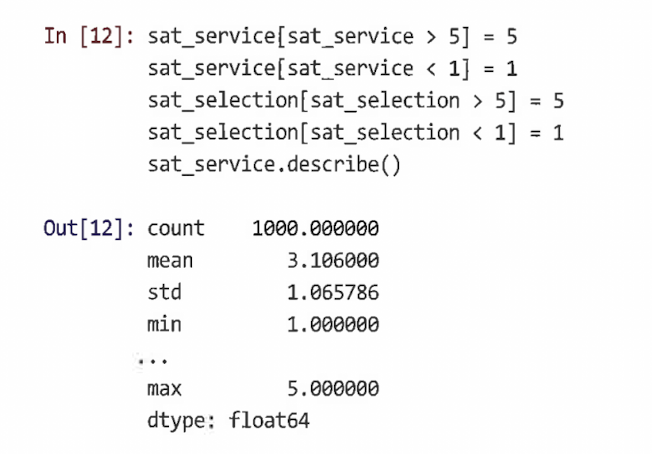
• sat_overall, numpy.floor()를 사용하여 연속 임의의 값을 불연속 정수로 변환
• 상한선 설정

4.1.4 무응답 데이터 시뮬레이션

고령고객은 설문조사에서 응답하지 않을 가능성이 높다고 가정하여 numpy.nan 값 할당

4.2 산점도가 있는 변수 간의 연관성 탐색

4.2.1 plot()

치우친 데이터 분포의 경우 히스토그램으로 연관성을 분석하는 것이 더 좋은 방법이다

 

4.4 산점도 행렬

4.4.1 scatter_matrix()

• padnas.plotting.scatter_matrix(dataframe) 
• 반환된 객체의 자동출력을 억제하기 위해'_'설정

4.4.2 PairGrid()

scatter_matrix()보다 데이터 쌍 관계를 탐색하기에 좋음

• size 인수로 각 패널 크기 설정, hue_kws 인수에 마커 목록 전달
• 데이터 그려지는 방식을 정의하기 위해 맵 정의 

4.5 상관계수 

변수가 많을 때는 각 쌍의 관계를 단일 숫자로 평가하는 것이 유용

두 변수 간의 관계를 측정하는 척도 중 하나는 공분산

np.cov() 함수를 사용해 공분산 계산

• 공분산이란?

두 변수가 평균보다 높거나 낮은 정도를 측정함으로써 변수가 함께 변하는 정도를 나타냄

 

분산 공식

두 변수가 같도록 X를 Y로 바꾸어 두 변수가 같도록 변형

공분산 공식

X와 Y가 독립이라면, 각 항이 0이 되므로 공분산은 0이 됨 -> 두 변수 간의 연관성이 없음

양의 공분산을 갖는 경우 둘의 관계가 양의 관계를 갖는 것

ex)x가 평균보다 클 때 y가 평균보다 크거나, x가 평균보다 작을 때 y가 평균보다 작음

음의 공분산을 갖는 경우 둘의 관계가 음의 관계를 갖는 것

공분산은 척도가 관련된 변수에 따라 달라지기 때문에 (ex. 공분산 2515, 74.54)공분산의 크기를 해석하기 어려운 문제가 발생

각 변수에 대한 표준편차로 공분산을 척도화 하기 위해 피어슨 상관계수 r사용

np.corrcoef()를 통해 피어슨 상관계수 행렬 계산

 

• 피어슨 상관계수(r)이란?

[-1,+1] 범위에 속하는 연속척도

두 변수 간의 완전한 양의 선형관계인 경우 +1, 완전한 음의 선형관계인 경우 -1, 선형 연관성이 거의 없으면 0에 가까워짐

 

 

 

4.5.1 상관관계검정

np.corrcoef(age, credit_score)에서 나온 r=0.29가 통계적으로 유의미한 것인가를 검정해보자

상관분석에서는 귀무가설 자체가 "상관 계수는 0이다."이기 때문에 p-value가 0.05미만일 때에만 상관계수가 의미를 가지게 됨

귀무가설이란 처음부터 버릴 것을 예상하는 가설

의미있는 차이가 없는 경우의 가설이며 이것이 맞거나 맞지 않다는 통계학적 증명을 통해 해당 가설 배제

양쪽 p의 값이 0에 매우 가깝기 때문에 귀무가설을 기각할 수 있음. r의값이 0.29처럼 중간 크기 효과라면 이러한 상관관계분석이 후속 단계에서 필요

 

4.5.2 상관행렬

2개 변수 이상의 경우 pandas의 corr()메서드를 사용하여 상관행렬 출력

• colorbar(), heatmap()을 통해 상관관계 시각화 가능

 

4.5.3 상관관계를 계산하기 전에 변수 변환

distance_to_store, store_spend 고객이 상점으로 이동하는 횟수, 상점으로부터 거리의 변화는 서로 반비례관계

역제곱근하면 거리가 멀어질수록 상점에 가는 횟수가 줄어드는 변수간의 관계가 더욱 명확해진다. 

산점도를 만들기전 변수를 정규성을 근사화하도록 변환하는 것을 고려해보는 것이 중요

 

4.5.4 일반적인 마케팅에서의 데이터 변환

마케팅 데이터(개수, 매출, 수익 등) 에서 자주 사용되는 몇 가지 일반적인 변환

 

 

4.5.5 박스-콕스 변환

박스-콕스 변환의 주된 용도는 임의의 데이터 분포를 정규 분포에 가깝게 만들거나 데이터 분산을 안정화하는 것으로 정규성을 근사화하는 변환

람다가 0일 때와 0이 아닐 때로 구분하여 데이터 y에 대해서 람다가 하나 주어지면 하나의 함수 변환이 되는 것 즉, 람다는 하나의 파라미터로 볼 수 있다.(어떤 람다를 쓰냐에 따라 함수 변환이 달라진다)

람다는 임의의 값을 취할 수 있기 때문에 정규 분포에 가장 잘 맞는 람다 값을 찾는 것이 목적 

변환된 데이터는 r에 대한 상관관계 강도를 해석하는데 더욱 효과적

• scipy.stats.boxcox()함수로 최적의 람다를 계산

• 박스-콕스 변환을 했을 때와 안 했을 때의 차이 비교 히스토그램

• 박스-콕스 변환된 변수값의 상관관계와 원시 데이터 상관관계 비교

상점까지의 거리와 지출 사이 관계는 더욱 강한 음의관계로 표현됨

 

4.6 설문 응답에서 연관성 탐색

순서 변수의 경우(ex. 고객이 5점 또는 7점의 점수를 준 경우) 변수 간의 연관성을 파악하는 것이 어려움 

plt.scatter()로 간단한 plot을 그린 경우 1에서 5까지의 정수값만 사용하므로 동일한 응답을 한 고객에 대한 점수가 겹쳐져 정확한 관측과 연관의 강도를 평가하는데 어려움

4.6.1 지터 : 서수 도면을 더 유익하게 만들기 

순서를 가지는 변수 값의 도면을 더욱 유용하게 만드는 방법 중 하나는 각 변수를 조금 흔들어 각 응답에 소량의 랜덤 노이즈를 추가하는 것 

이렇게 하면 점이 서로 멀어지고 (x,y)값의 각 조합에서 발생하는 응답 수가 표시됨

np.random.normal() 를 사용하여 n_cust 수의 난수를 생성한다.

 

평점 (3,2)및(3,3)이 가장 일반적인 응답, 두 만족도 변수는 양의 관계 가지는 것을 확인