문제 링크 : https://www.acmicpc.net/problem/1149
난이도 : 실버 1
1149번: RGB거리
첫째 줄에 집의 수 N(2 ≤ N ≤ 1,000)이 주어진다. 둘째 줄부터 N개의 줄에는 각 집을 빨강, 초록, 파랑으로 칠하는 비용이 1번 집부터 한 줄에 하나씩 주어진다. 집을 칠하는 비용은 1,000보다 작거나
www.acmicpc.net
문제
RGB거리에는 집이 N개 있다. 거리는 선분으로 나타낼 수 있고, 1번 집부터 N번 집이 순서대로 있다.
집은 빨강, 초록, 파랑 중 하나의 색으로 칠해야 한다. 각각의 집을 빨강, 초록, 파랑으로 칠하는 비용이 주어졌을 때, 아래 규칙을 만족하면서 모든 집을 칠하는 비용의 최솟값을 구해보자.
- 1번 집의 색은 2번 집의 색과 같지 않아야 한다.
- N번 집의 색은 N-1번 집의 색과 같지 않아야 한다.
- i(2 ≤ i ≤ N-1)번 집의 색은 i-1번, i+1번 집의 색과 같지 않아야 한다.
입력
첫째 줄에 집의 수 N(2 ≤ N ≤ 1,000)이 주어진다. 둘째 줄부터 N개의 줄에는 각 집을 빨강, 초록, 파랑으로 칠하는 비용이 1번 집부터 한 줄에 하나씩 주어진다. 집을 칠하는 비용은 1,000보다 작거나 같은 자연수이다.
출력
첫째 줄에 모든 집을 칠하는 비용의 최솟값을 출력한다.
😅 (잘못된) 풀이 접근법
예시 테케 2개 정도만 써보면서 열은 항상 3개씩 밖에 존재하지 않으니깐
그냥 단순히 전에 선택했던 색깔을 빼고 둘 중 작은 수를 고르면 되는거 아닌가!?
시간복잡도도 O(N)밖에 안걸리는데?!!?!
하고 그냥 RGB 리스트 만들어서 값을 비교하는 형식으로 처리했당.. ^^,,
안 좋은 코드의 예 😮💨 )
# 틀린 풀이
N = int(input())
arr = [list(map(int, input().split())) for _ in range (N)]
rgb = [0, 1, 2]
ans = min(arr[0])
j = arr[0].index(min(arr[0]))
rgb.pop(j)
for r in range (1, N) :
temp1 = arr[r][rgb[0]]
temp2 = arr[r][rgb[1]]
if temp1 < temp2 :
c = rgb[0]
ans += temp1
else :
c = rgb[1]
ans += temp2
rgb = [0,1,2]
rgb.pop(c)
print(ans)
ㅎㅎㅎㅎㅎ 예시 8번 케이스에서 딱 걸려버렸다.
8
71 39 44
32 83 55
51 37 63
89 29 100
83 58 11
65 13 15
47 25 29
60 66 19
answer) 253
output) 310
항상 작은 수를 선택하는 것이 최적의 경우가 아니구나..!! (그리디? 로 접근하면 안된다.)
그렇다면 또 완탐을 꺼내야하나..??
그렇게 되면 모든 행마다 선택할 수 있는 경우가 2개씩인데,
시간복잡도를 따지면, 최악의 경우 집이 1,000개일 때 2^1,000이 돼버린다.(즉, O(2^N)) 완전 시간초과 대박
그래서 dfs로는 풀면 안됨
이 문제는 dp로 해결할 수 있는 문제였다..
왜냐????? 규칙을 찾으면 dp문제인 것을 이해할 수 있는데,
dp 를 사용할 수 있는 조건에 부합하는지 검사해보면
1) 큰 문제를 작은 문제로 쪼갤 수 있는가?
-> 넵. N행까지 모두 더한 최소 비용은 N 이전 행까지의 최소 비용 문제로 쪼개볼 수 있다.
2) 작은 문제에서 구한 정답은 그것을 포함하는 큰 문제에서도 동일한가?
-> yes! 이전 집까지 최소 비용 결과에 현재 집의 값을 더해서 최소 비용을 갱신하게 되므로
이전의 결과를 그대로 가져와서 사용한다고 볼 수 있다.
즉, 집에 하나씩 색을 칠하면서 누적된 최소 비용값을 dp테이블에 저장하고
마지막 집까지 도달했을 때, 가장 작은 비용 값을 정답으로 출력하면 된다.
그림으로 나타내면 다음과 같다!
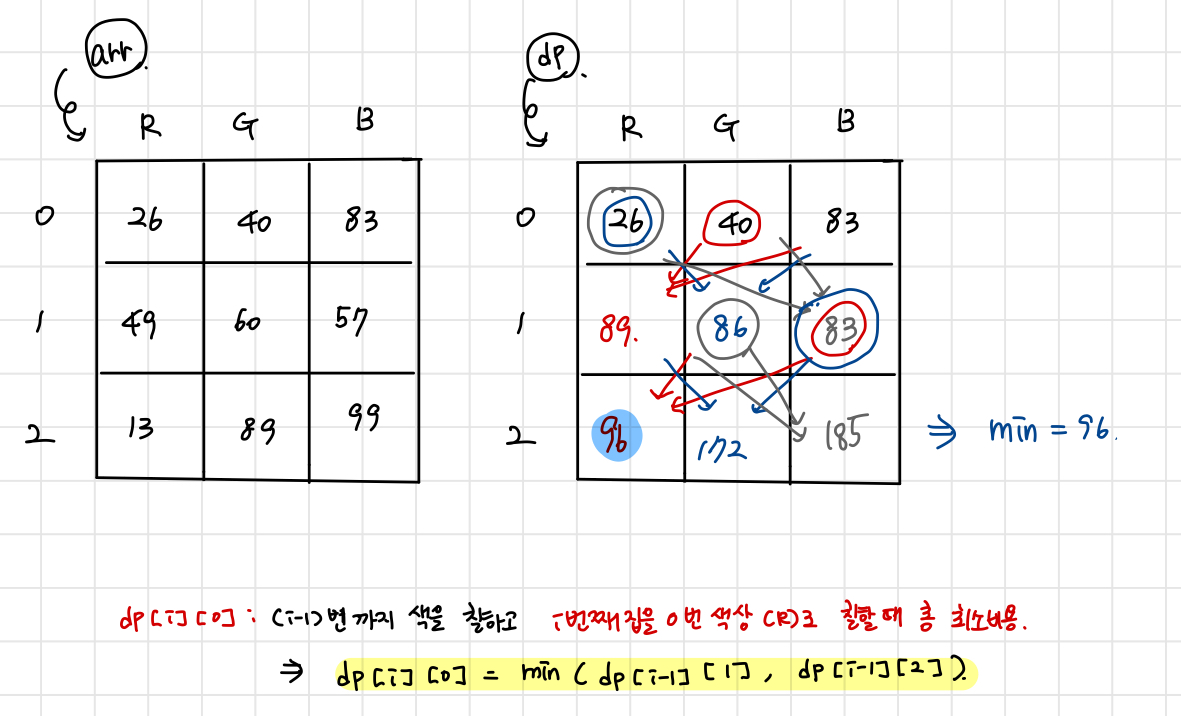
이 규칙을 점화식으로 나타내면
dp[i][0] = min(dp[i-1][1], dp[i-1][2]) : i번째 집을 0번째 색깔로 칠하는 경우
이 패턴으로 1, 2번 색깔로 칠하는 경우에 대해서도 값을 갱신해주면 된다!!
📌 정답 코드
N = int(input())
arr = [list(map(int, input().split())) for _ in range (N)]
# 최소 비용을 저장하는 dp 테이블
dp = [[0] * 3 for _ in range (N)]
# dp 초기값 설정(첫번째 행은 그대로)
dp[0] = arr[0]
# 보텀업
for i in range (1, N) :
# dp[i][color] : i번째 집을 color로 칠했을 때 총 최소 비용
dp[i][0] = min(dp[i-1][1], dp[i-1][2]) + arr[i][0] #R로 색칠
dp[i][1] = min(dp[i-1][0], dp[i-1][2]) + arr[i][1] #G로 색칠
dp[i][2] = min(dp[i-1][0], dp[i-1][1]) + arr[i][2] #B로 색칠
print(min(dp[N-1]))
코드 짤 때 주어진 예시 테케는 다 따져보면서 반례를 빨리 찾아낼 것.. ✍️
✅ 2월두 아자아자 화팅이댯~!!

'알고리즘' 카테고리의 다른 글
| [백준 11660번] 구간 합 구하기 5 (Python) (2) | 2024.02.02 |
|---|---|
| [백준 1463번] 1로 만들기(Python) (0) | 2024.01.30 |
| [삼성 SW 역량 테스트 기출] 백준 14888번 연산자 끼워넣기(Python) (1) | 2024.01.30 |
| [삼성 SW 역량테스트 기출] 백준 14500번 테트로미노(Python) (1) | 2024.01.29 |
| [백준 1904번] 01타일(Python) (1) | 2024.01.29 |
