문제 링크 : https://www.acmicpc.net/problem/11660
난이도 : 실버 1
11660번: 구간 합 구하기 5
첫째 줄에 표의 크기 N과 합을 구해야 하는 횟수 M이 주어진다. (1 ≤ N ≤ 1024, 1 ≤ M ≤ 100,000) 둘째 줄부터 N개의 줄에는 표에 채워져 있는 수가 1행부터 차례대로 주어진다. 다음 M개의 줄에는 네
www.acmicpc.net
문제
N×N개의 수가 N×N 크기의 표에 채워져 있다. (x1, y1)부터 (x2, y2)까지 합을 구하는 프로그램을 작성하시오. (x, y)는 x행 y열을 의미한다.
예를 들어, N = 4이고, 표가 아래와 같이 채워져 있는 경우를 살펴보자.
| 1 | 2 | 3 | 4 |
| 2 | 3 | 4 | 5 |
| 3 | 4 | 5 | 6 |
| 4 | 5 | 6 | 7 |
여기서 (2, 2)부터 (3, 4)까지 합을 구하면 3+4+5+4+5+6 = 27이고, (4, 4)부터 (4, 4)까지 합을 구하면 7이다.
표에 채워져 있는 수와 합을 구하는 연산이 주어졌을 때, 이를 처리하는 프로그램을 작성하시오.
입력
첫째 줄에 표의 크기 N과 합을 구해야 하는 횟수 M이 주어진다. (1 ≤ N ≤ 1024, 1 ≤ M ≤ 100,000) 둘째 줄부터 N개의 줄에는 표에 채워져 있는 수가 1행부터 차례대로 주어진다. 다음 M개의 줄에는 네 개의 정수 x1, y1, x2, y2 가 주어지며, (x1, y1)부터 (x2, y2)의 합을 구해 출력해야 한다. 표에 채워져 있는 수는 1,000보다 작거나 같은 자연수이다. (x1 ≤ x2, y1 ≤ y2)
출력
총 M줄에 걸쳐 (x1, y1)부터 (x2, y2)까지 합을 구해 출력한다.
📌 풀이 접근 방법
행렬에 수만 누적해서 더해주면 되기 때문에 되게 간단해보이는 문제지만, 변수들의 범위가 심상치 않다...
일일히 다 탐색 -> 시간 초과 나게 하려구 낸 문제 😅
최악의 경우, 최대 맵 크기(NxN) 내에서 모두 탐색하면서 연산 횟수(M) 만큼 계산하게 되면
1,024 x 1,024 x 100,000 으로 문제를 풀지 못하게 된다.
역시나 dp 구나..
요즘 dp 문제만 걸려들여서... 좋다..
특정 구간의 합을 구하기 위해서는 (1,1) 부터 (x2, y2)까지의 누적 합을 dp 테이블에 저장해둔 뒤,
(x2, y2)까지의 누적 합에서 구간에 해당하지 않는 부분은 빼주면 된다!
이 때 중복되면서 2번 빼주는 구간이 발생하기 때문에, 이 구간은 한 번 더해줘야한다.
그림으로 보면 이해하기 쉬울 것이당.
다음과 같은 예시가 있다고 하면,
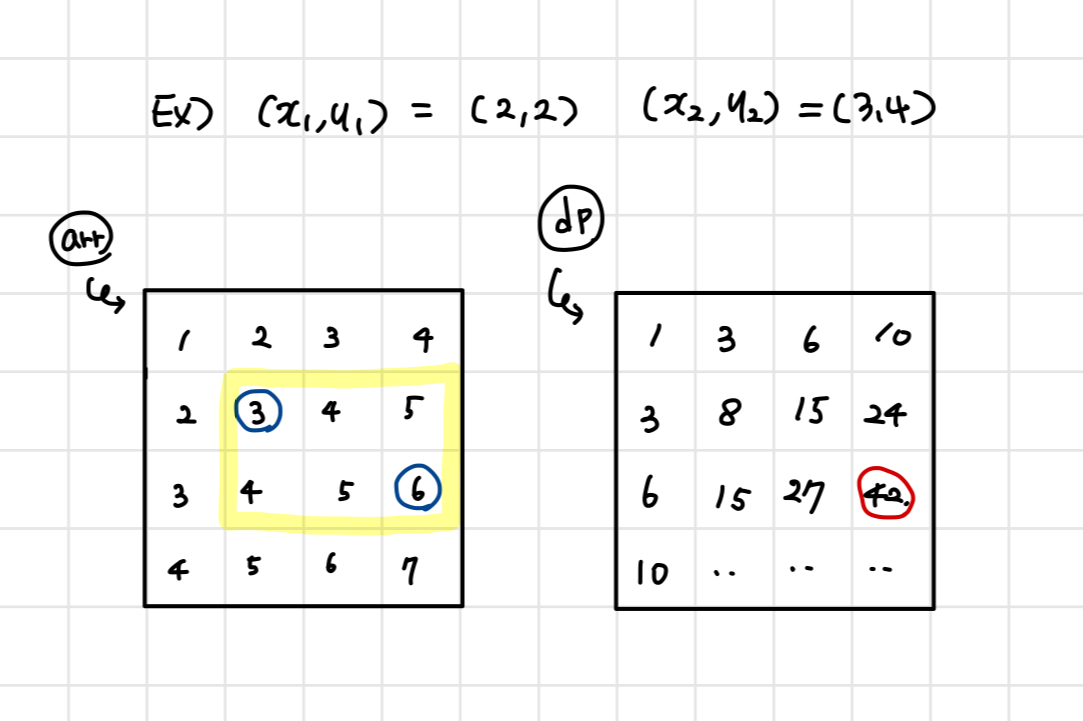
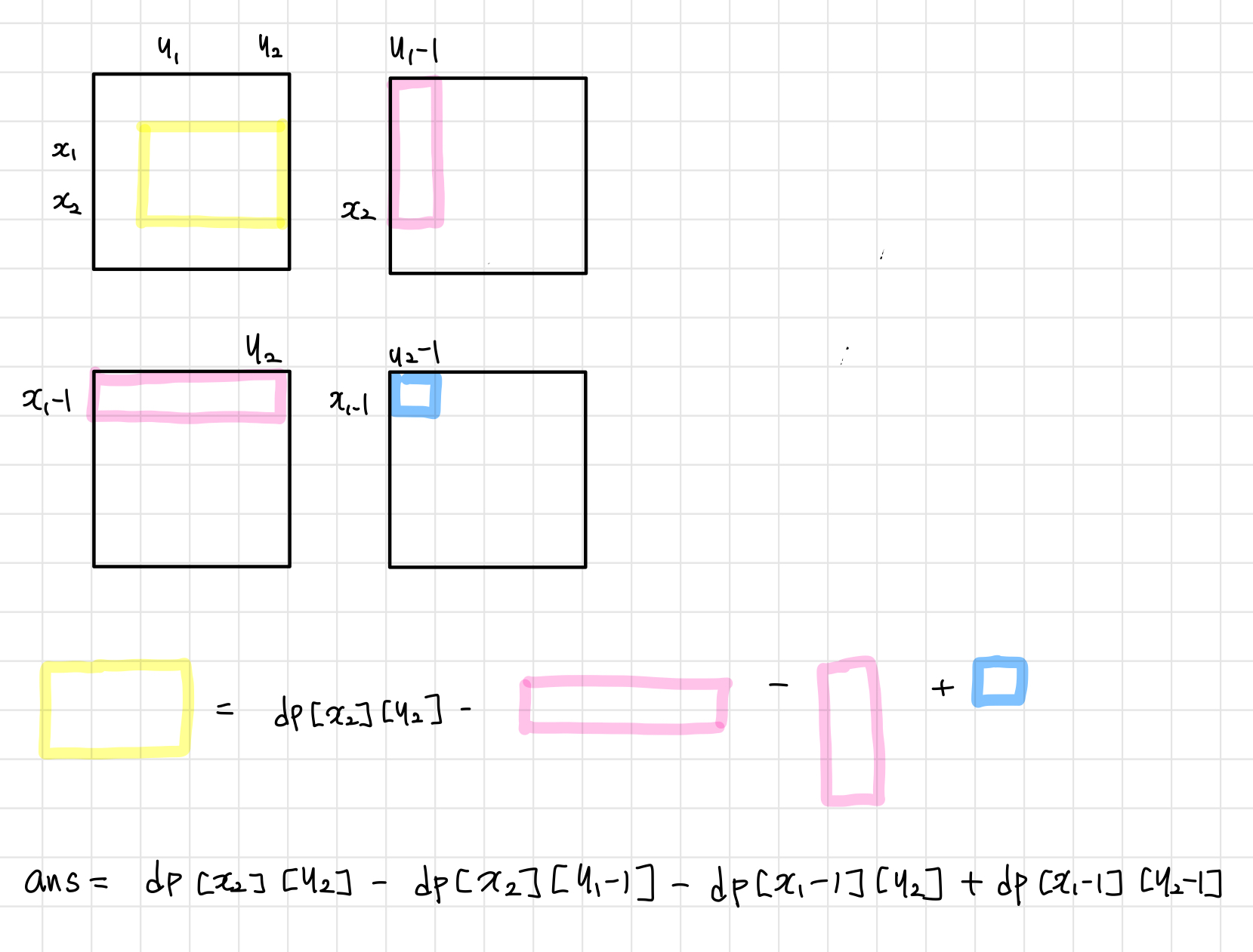
이를 점화식으로 나타내면 위의 노트에 적어둔 것과 같다.
즉, dp 테이블의 누적 합을 구할 때 각 요소를 일일히 하나씩 더해주는 것이 아닌
보텀업 방식으로 dp테이블을 구성하여 이전에 계산되었던 누적 합들을 그대로 가져오면서 코드가 더 효율적으로 동작하게 되는 것이다!
📌 정답 코드
import sys
input = sys.stdin.readline
# 정답 풀이
N, M = map(int, input().split())
arr = [list(map(int, input().split())) for _ in range(N)]
dp = [[0] * (N+1) for _ in range (N+1)]
# 누적합 dp 계산(보텀업)
for i in range (1, N+1) :
for j in range (1, N+1) :
dp[i][j] = dp[i][j-1] + dp[i-1][j] - dp[i-1][j-1] + arr[i-1][j-1]
# 원하는 구간 계산
for _ in range (M) :
x1, y1, x2, y2 = map(int, input().split())
ans = dp[x2][y2] - dp[x1-1][y2] - dp[x2][y1-1] + dp[x1-1][y1-1]
print(ans)
sys 모듈 사용하면 입력 값들을 더 빨리 처리하기 때문에 시간초과를 방지할 수 있다!
'알고리즘' 카테고리의 다른 글
| [백준 1149] RGB 거리(Python) (0) | 2024.02.01 |
|---|---|
| [백준 1463번] 1로 만들기(Python) (0) | 2024.01.30 |
| [삼성 SW 역량 테스트 기출] 백준 14888번 연산자 끼워넣기(Python) (1) | 2024.01.30 |
| [삼성 SW 역량테스트 기출] 백준 14500번 테트로미노(Python) (1) | 2024.01.29 |
| [백준 1904번] 01타일(Python) (1) | 2024.01.29 |
문제 링크 : https://www.acmicpc.net/problem/11660
난이도 : 실버 1
11660번: 구간 합 구하기 5
첫째 줄에 표의 크기 N과 합을 구해야 하는 횟수 M이 주어진다. (1 ≤ N ≤ 1024, 1 ≤ M ≤ 100,000) 둘째 줄부터 N개의 줄에는 표에 채워져 있는 수가 1행부터 차례대로 주어진다. 다음 M개의 줄에는 네
www.acmicpc.net
문제
N×N개의 수가 N×N 크기의 표에 채워져 있다. (x1, y1)부터 (x2, y2)까지 합을 구하는 프로그램을 작성하시오. (x, y)는 x행 y열을 의미한다.
예를 들어, N = 4이고, 표가 아래와 같이 채워져 있는 경우를 살펴보자.
| 1 | 2 | 3 | 4 |
| 2 | 3 | 4 | 5 |
| 3 | 4 | 5 | 6 |
| 4 | 5 | 6 | 7 |
여기서 (2, 2)부터 (3, 4)까지 합을 구하면 3+4+5+4+5+6 = 27이고, (4, 4)부터 (4, 4)까지 합을 구하면 7이다.
표에 채워져 있는 수와 합을 구하는 연산이 주어졌을 때, 이를 처리하는 프로그램을 작성하시오.
입력
첫째 줄에 표의 크기 N과 합을 구해야 하는 횟수 M이 주어진다. (1 ≤ N ≤ 1024, 1 ≤ M ≤ 100,000) 둘째 줄부터 N개의 줄에는 표에 채워져 있는 수가 1행부터 차례대로 주어진다. 다음 M개의 줄에는 네 개의 정수 x1, y1, x2, y2 가 주어지며, (x1, y1)부터 (x2, y2)의 합을 구해 출력해야 한다. 표에 채워져 있는 수는 1,000보다 작거나 같은 자연수이다. (x1 ≤ x2, y1 ≤ y2)
출력
총 M줄에 걸쳐 (x1, y1)부터 (x2, y2)까지 합을 구해 출력한다.
📌 풀이 접근 방법
행렬에 수만 누적해서 더해주면 되기 때문에 되게 간단해보이는 문제지만, 변수들의 범위가 심상치 않다...
일일히 다 탐색 -> 시간 초과 나게 하려구 낸 문제 😅
최악의 경우, 최대 맵 크기(NxN) 내에서 모두 탐색하면서 연산 횟수(M) 만큼 계산하게 되면
1,024 x 1,024 x 100,000 으로 문제를 풀지 못하게 된다.
역시나 dp 구나..
요즘 dp 문제만 걸려들여서... 좋다..
특정 구간의 합을 구하기 위해서는 (1,1) 부터 (x2, y2)까지의 누적 합을 dp 테이블에 저장해둔 뒤,
(x2, y2)까지의 누적 합에서 구간에 해당하지 않는 부분은 빼주면 된다!
이 때 중복되면서 2번 빼주는 구간이 발생하기 때문에, 이 구간은 한 번 더해줘야한다.
그림으로 보면 이해하기 쉬울 것이당.
다음과 같은 예시가 있다고 하면,


이를 점화식으로 나타내면 위의 노트에 적어둔 것과 같다.
즉, dp 테이블의 누적 합을 구할 때 각 요소를 일일히 하나씩 더해주는 것이 아닌
보텀업 방식으로 dp테이블을 구성하여 이전에 계산되었던 누적 합들을 그대로 가져오면서 코드가 더 효율적으로 동작하게 되는 것이다!
📌 정답 코드
import sys
input = sys.stdin.readline
# 정답 풀이
N, M = map(int, input().split())
arr = [list(map(int, input().split())) for _ in range(N)]
dp = [[0] * (N+1) for _ in range (N+1)]
# 누적합 dp 계산(보텀업)
for i in range (1, N+1) :
for j in range (1, N+1) :
dp[i][j] = dp[i][j-1] + dp[i-1][j] - dp[i-1][j-1] + arr[i-1][j-1]
# 원하는 구간 계산
for _ in range (M) :
x1, y1, x2, y2 = map(int, input().split())
ans = dp[x2][y2] - dp[x1-1][y2] - dp[x2][y1-1] + dp[x1-1][y1-1]
print(ans)
sys 모듈 사용하면 입력 값들을 더 빨리 처리하기 때문에 시간초과를 방지할 수 있다!
'알고리즘' 카테고리의 다른 글
| [백준 1149] RGB 거리(Python) (0) | 2024.02.01 |
|---|---|
| [백준 1463번] 1로 만들기(Python) (0) | 2024.01.30 |
| [삼성 SW 역량 테스트 기출] 백준 14888번 연산자 끼워넣기(Python) (1) | 2024.01.30 |
| [삼성 SW 역량테스트 기출] 백준 14500번 테트로미노(Python) (1) | 2024.01.29 |
| [백준 1904번] 01타일(Python) (1) | 2024.01.29 |
