{학습 목적}
Part 1에서는 판매처에서 물품을 구매하여 만족할 확률을 예시로 들어 성공률에 대한 이항분포를 설명하고 있다.
이 부분을 학습하는 이유는 어떤 성공 확률이 얼마나 가능성이 있는 확률인지 즉 확률의 확률에 대해 알기 위한 바탕 지식을 공부하기 위해서라고 생각한다.
<수학적으로 어느 별점이 더 나은 걸까?(이항 분포에 관해서)>
어떤 제품을 온라인 쇼핑몰에서 사려 하는 데 판매처가 세 곳이 있다.
똑같은 제품을 같은 가격에 팔고 있다고 하자
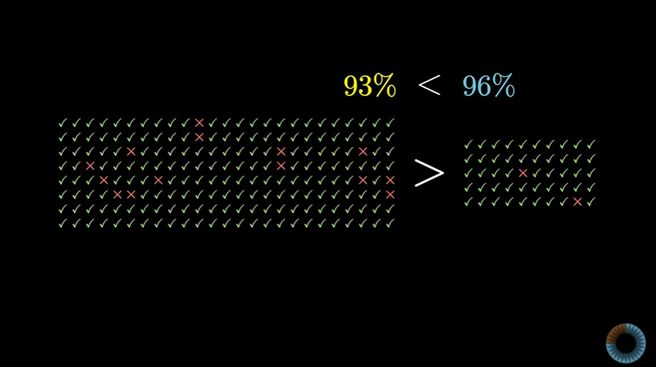
첫 판매처는 10건의 리뷰가 100퍼센트 만족을 나타내고
2번째 판매처는 50건의 리뷰가 96퍼센트의 만족을
3번째 판매처는 200건의 리뷰가 93퍼센트의 만족을 나타낸다. 어디서 사는 게 좋을까?
아마 다들 리뷰가 더 많으면 많을수록 더 신뢰할 수 있다고 생각할 것이다.
보통 리뷰의 수가 적으면 몇 건만 달라져도 더 낮은 만족도를 보일 수 있기 때문이다.

이처럼 더 많은 리뷰 건수와 더 높은 만족도 중에 무엇이 더 유용한 지표인지 어떻게 판단할까?
10명 중 10명 모두 만족해 하는 온라인 리뷰를 보면 하나는 만족, 다른 하나는 불만족인 두 리뷰가 더 있을 것이라고 생각하자
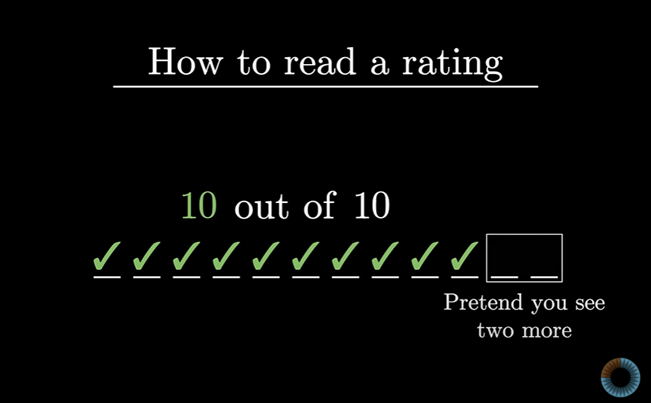
이 경우에는 11/12 만족 즉 91.7% 만족이라고 보는 것이다.
이것이 우리가 판매처에서 제품을 살 때 만족할 확률이다.

50건의 리뷰 중 48건 만족, 2건 불만족인 경우
52건의 리뷰 중 49건 만족, 3건 불만족이라고 보는 것이다.
그러면 49/52 즉 94.2%만족이라는 의미이다.
이것이 두 번째 판매처에서 샀을 때의 만족할 확률이다.

200건의 리뷰가 있는 3번째 판매처에서도 똑같이 하면 187/202점을 얻는다.
즉 만족 92.6%이다.
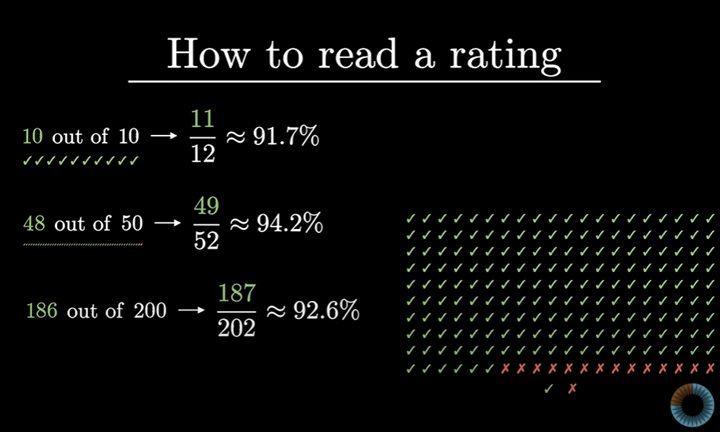
이 규칙대로 라면 2번째 판매처의 만족 확률이 가장 높은 것으로 확인할 수 있다.
이를 라플라스 성공법칙이라고 한다.
이제까지 어떤 한 상황설명을 끝냈다.
이제 본격적으로 이항 분포에 대해 알아보도록 한다.
[이항 분포]
1단계. 우리가 얼마나 정확하게 상황을 모델링 하고 있고 우리가 생각하는 ‘최적의 결과’란 무엇인가?
가능한 한 가지 모델은 판매처는 구매자에게 무작위로 긍정적이거나 부정적인 경험을 제공한다고 보는 것이다.
그리고 각 판매처는 일정 확률로 긍정적 경험을 선사한다.
이것을 성공 확률 ‘s’라고 쓴다. (s = 만족 리뷰를 얻을 확률)
문제는 우리는 s 값을 모른다는 것이다.
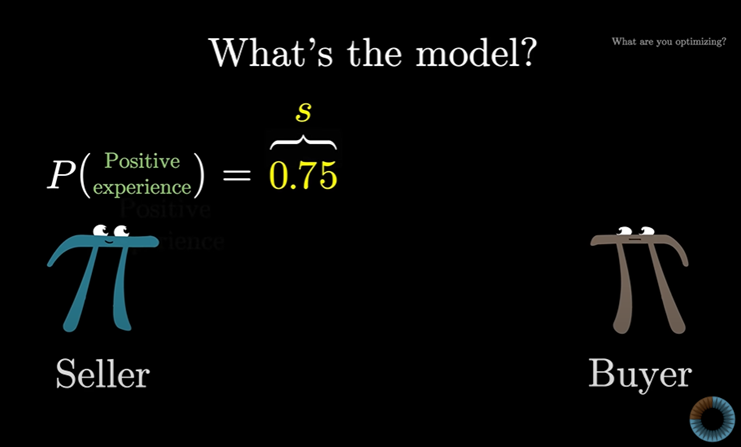
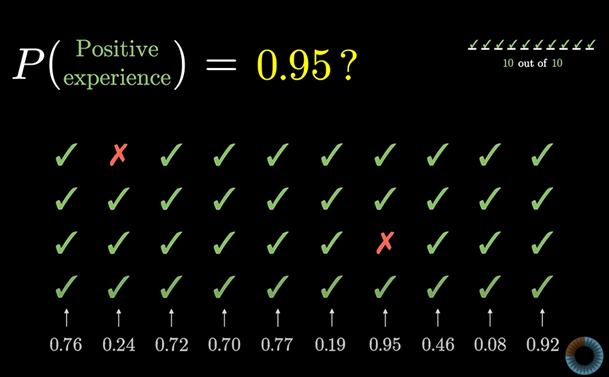
10/10 의 첫 번째 리뷰가 s 값이 100%라는 말이 아니다. 어쩌면 95%가 될 수도 있다.
0과 1 사이에서 고른 임의의 수가 0.95보다 작다면 ‘만족’ 리뷰를 그렇지 않으면 ‘불만족’ 리뷰를 남긴다고 해보자.
이것을 10번 반복하고 10번 더 반복하는 것을 계속하면 이 성공률 95%의 판매처의 이용자들이 남긴 각 10건의 리뷰 결과는 어떻게 될까?
60% 정도는 10/10을 기록했다.
그러면 이 데이터가 나타내는 판매처의 성공률은 95%쯤 된다는 것은 그럴 듯 해 보인다.

어쩌면 90%나 99%일지도 모르겠지만 결국 문제는 우리가 성공확률을 모른다는 데 있다.
우리의 목표는 성공확률을 정확히 알 순 없지만 성공확률을 최대화 하는 것이라고 하자
각 판매처에 대해 가능한 성공할 확률은 0에서 1사이로 많다.
우리는 각 성공률이 얼마나 가능성이 있는지 알아야 한다.(확률의 확률)
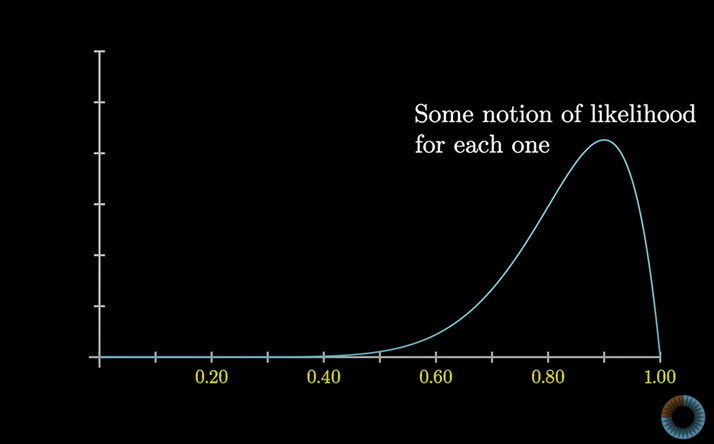
동전 던지기, 주사위 굴리기 같은 사례는 보통 장기적 빈도(확률)로 1/2이나 1/6따위를 얻지만
지금 우리가 다루는 건 확률 그 자체의 불확실성이다.
또한 우리는 이 상황을 무작위 사건에 대해 한정된 시행으로 판단해야한다.
만약 성공률이 95%라고 정해져있다면 10/10 리뷰 결과가 나올 확률은 얼마가 될까?
마찬가지로 48/50은? 186/200은?
다시 말해 s값이 주어졌을 때 어떤 리뷰 결과가 나올 확률은 얼마가 될까?

10건의 무작위 리뷰를 만들 때 이에 대한 분포가 어떻게 될 지 히스토그램을 쌓아보자

같은 방식으로 48/50은 어떻게 되는지 보기 위해 50건도 돌려보자
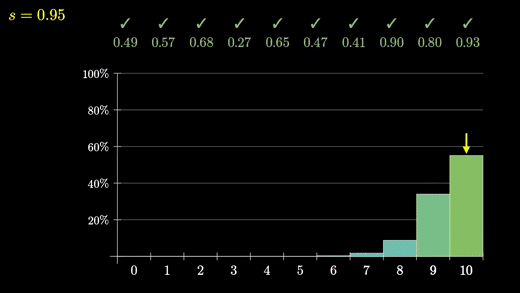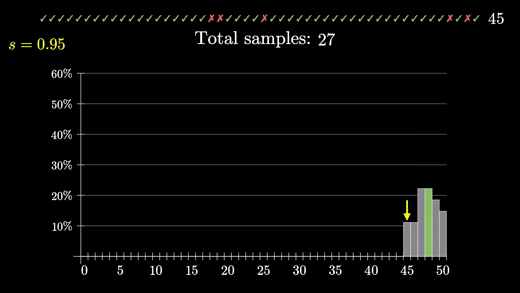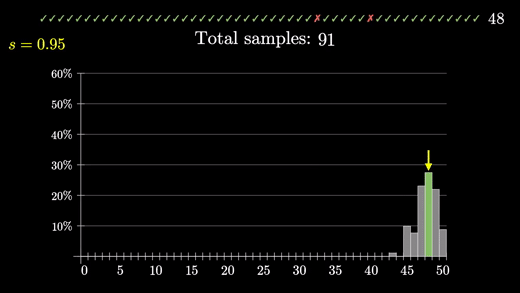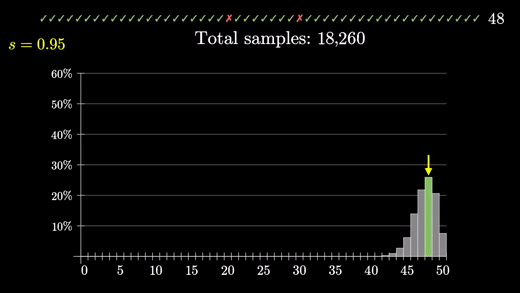
프로그래밍을 통해 성공률 95%면 48/50이 나올 확률은 대강 26.1%이다.
48/50이 나올 정확한 확률의 공식을 보자
앞부분은 “50 중 48 택”이라 읽는다. (한국에서는 50C48이라 흔히 쓰는 조합이다.)
50개의 칸을 48개로 채우는 모든 경우의 수를 말한다.
이렇게 50개의 빈칸을 48개로 채우는 경우의 수는 1225가지이다.
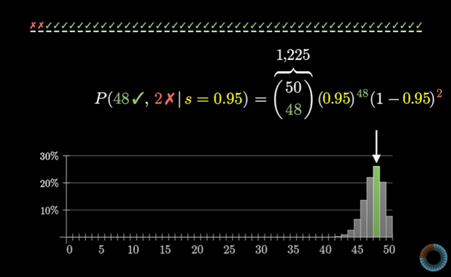
그 뒤에 각각 리뷰가 남겨질 확률을 곱한다.
(‘만족’리뷰를 남길 확률)^48 x (‘불만족’리뷰를 남길 확률)^2 이다.
각각의 리뷰가 그 전 리뷰와 독립적인 경우이다.
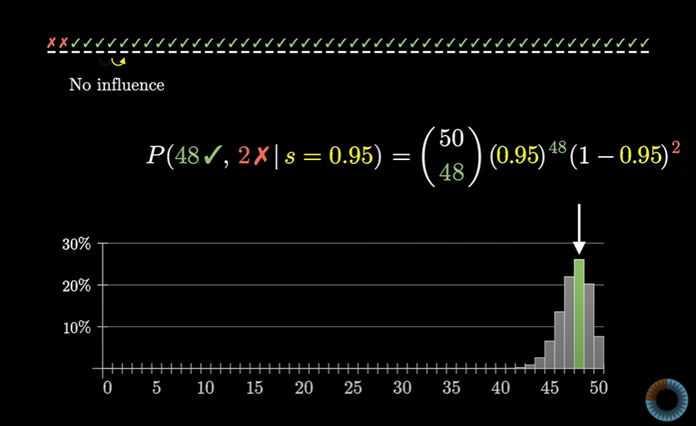
이걸 계산하면 0.261 쯤 된다.
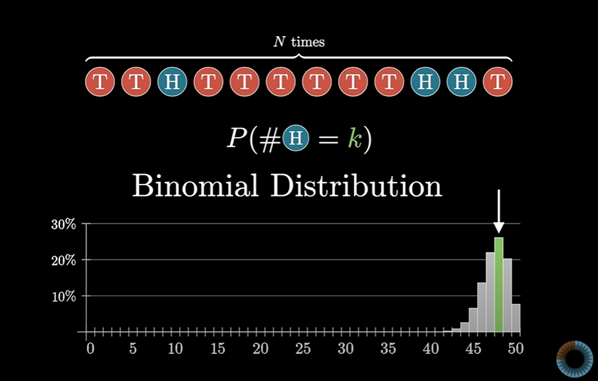
이것이 이항 분포(Binomial Distribution)의 예시이다.
이항 분포는 확률론에서 가장 기본적인 분포 중 하나이다.
동전 던지기처럼 두 가지 결과가 있는 확률적 사건을 몇 번 반복했을 때 어떤 결과를 얻을 확률을 구하기 위해 이항 분포가 쓰인다.
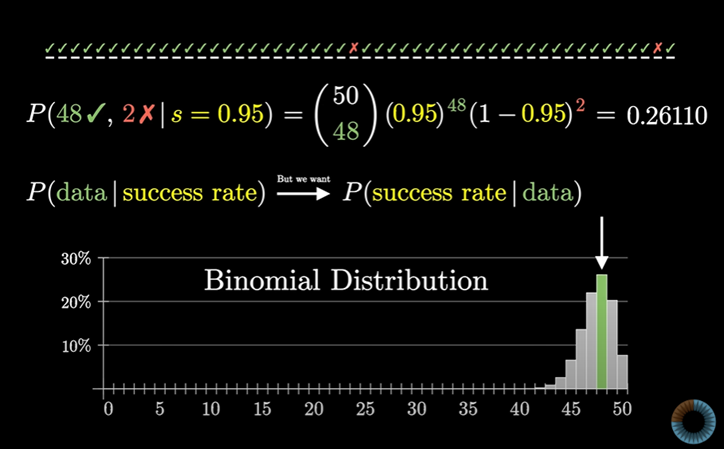
앞에서 본 예시의 경우 성공 확률이 주어졌을 때 특정 리뷰 데이터가 나올 확률을 구하는 데 쓰였다.
하지만 우리가 알고자 하는 건 반대로 어떤 리뷰데이터가 있을 때 각 성공확률의 확률이다.
이 s값을 0과 1 사이 값으로 변환시켜가며 변화를 관찰해보자
이항 분포는 더미 모양을 나타내고 그 가운데 48/50의 결과가 나올 확률을 나타내는 녹색의 막대로 표시했다.
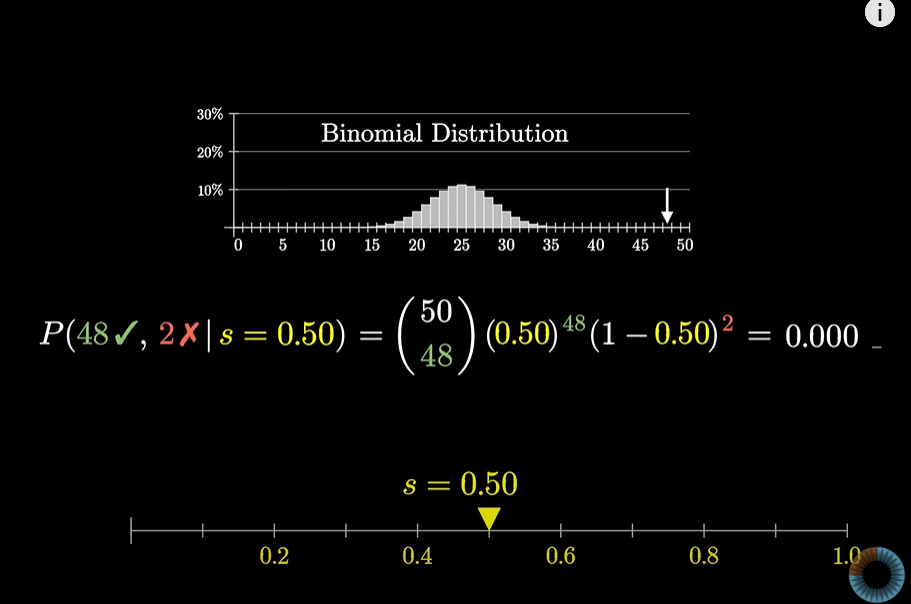
이 확률이 s값에 따라 어떻게 변하는지 표시해보면 s값이 0.96일 때 48/50결과가 나올 확률이 가장 높다.
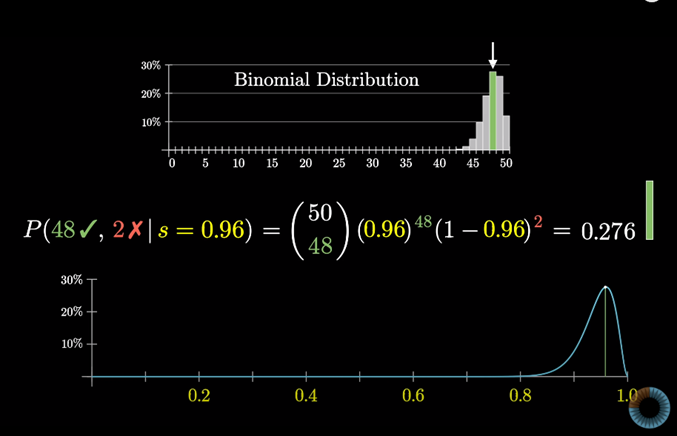
이것은 96% 긍정(48/50)이라는 리뷰를 볼 때 성공 확률이 96%쯤 되겠다고 생각하는 것으로 보아 납득이 가는 사실이다.
s가 0.96을 넘어서 증가하면 s가 1로 접근함에 따라 확률은 0이된다.
성공률이 100%면 불만족을 남기는 사람은 없기 때문이다. (50건의 리뷰 중 50건 모두 만족이 되는 경우임)
s가 0.8이 될 때쯤 48/50의 확률은 1000번에 1번 꼴로 매우 드물어진다.
즉, 아래의 그래프는 어떤 s가 우리가 원하는 결과가 나올 가능성이 있는지 설명하는 데 좋은 자료이다.
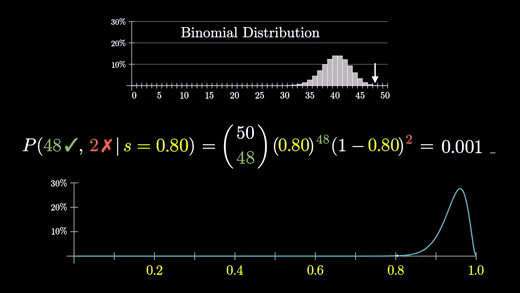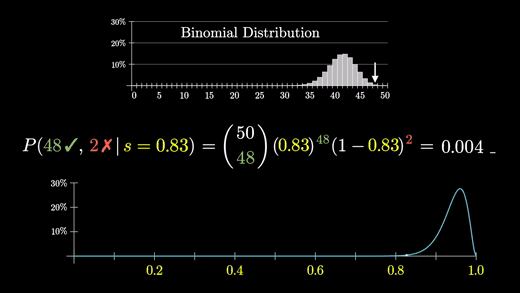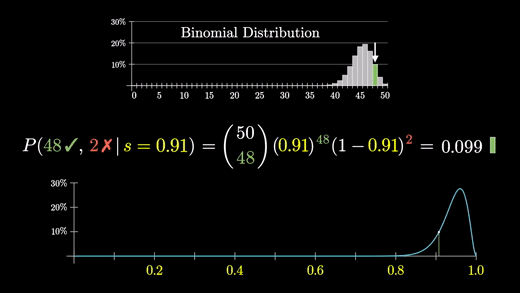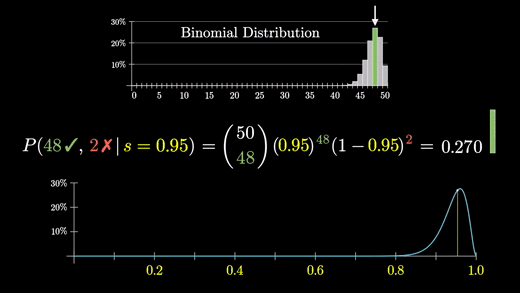
기억해야할 것은 성공률이 s라면 그래프는 (어떤 상수) x s^(만족 건수) x (1-s)^(불만족 건수)를 나타낸다는 것이다.
이 공식에 따르면 우리에게 480/500처럼 더 많은 리뷰가 주어질수록 s 값은 여전히 0.96안팎이지만 훨씬 더 정확해진다.

이 그래프를 가지고 무엇을 할 수 있을까?
원래 목표는 이 판매처에서 구매하면 만족할 확률(s)이 얼마나 될까를 구하는 거였다.
96%가 그래프의 꼭대기에 있기 때문에 확률은 96%라고 생각할 수 있다.
어떻게 보면 96%가 가장 가능성 있긴하다.
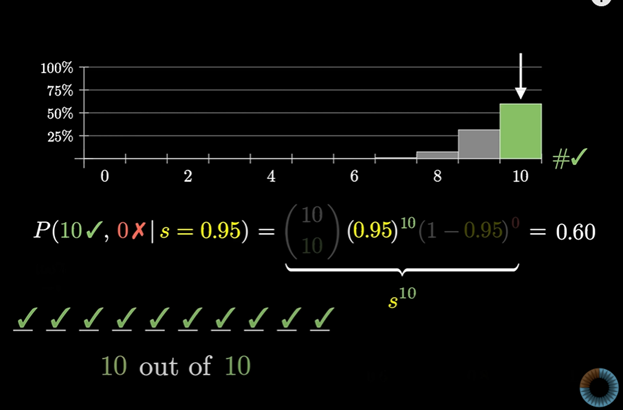
그렇지만 10/10 경우를 떠올려 보자
이 경우 분포 모두가 s가 1이라고 단순화 하는 셈이다. (만족할 확률 100%)
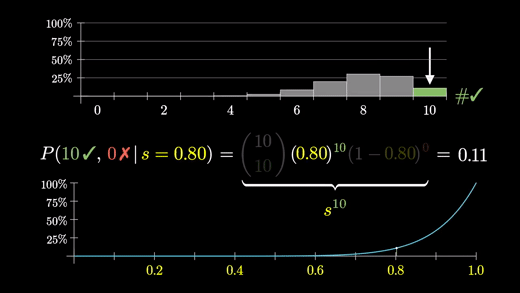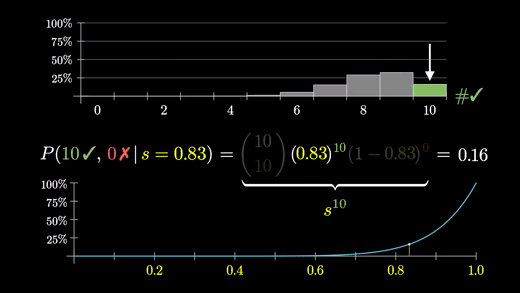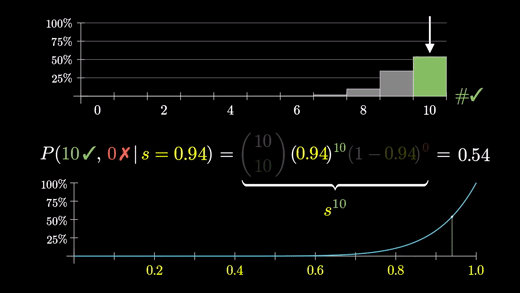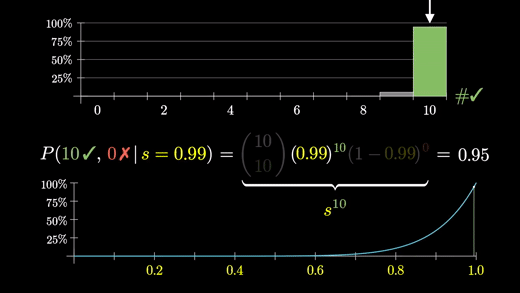
이 경우의 확률(10건 중 10건 다 만족할 확률)은 s의 10제곱인데 그러면 s가 1에 가까울수록 그 s가 옳을 확률도 커진다.
아래 그래프는 s가 1에 가까워질수록 증가만 하고 있다.
s=1 일 때의 10/10 확률이 가장 크긴 하지만 이 판매처에서 산 것이 무조건 100% 만족할 것이라고 생각하는 것은 조금 찝찝하다.
그래서 우리는 이럴 때 그래프의 무게 중심 쪽에 집중을 하게 될 것이다.
하지만 우선 s가 주어졌을 때 어떤 데이터를 얻을 확률을 어떤 데이터가 주어졌을 때 어떤 s가 참일 확률로 고쳐야한다.
이야기를 할려면 베이즈 정리와 확률밀도함수에 관한 얘기를 해야한다.
- 이항 분포?
- 두 가지 결과 (만족, 불만족 or 성공, 실패)가 있는 사건에서 특정 시행 횟수에서 어떤 결과가 나올 확률을 구할 때 쓰이는 분포
