{학습 목적}
Part 2 에서는 확률밀도함수에 대해서 학습한다.
이 부분을 학습하는 이유는 확률의 확률에 대한 역설을 해결하여 확률을 구하기 위해서이다.
동전을 던지는 시행을 생각해보자
앞면이 나올 확률은 20%, 90%, 0% .. 등 우리는 앞면이 나올 확률을 알지 못한다.
이 동전을 10번 던진다고 했을 때, 그 중 앞면이 7번 나온 경우를 보자
이것은 각 시행마다 앞면이 나올 확률이 0.7이라는 것과 같을까?
이것은 이상하게 느껴지는 질문이다.
먼저 확률의 확률 (앞면이 나올 확률이 0.7인가?)에 대해 묻고
우리가 앞면이 나올 빈도조차 모르기 때문이다.
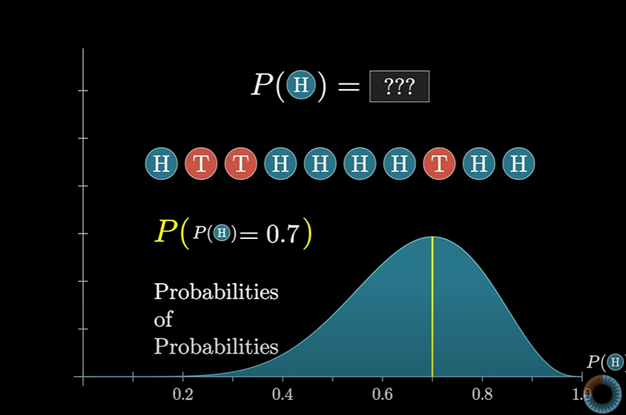
하지만 이 질문을 연속값의 맥락에서 본다면 답을 얻을 수 있다
앞면이 나올 확률을 "h"라고 해보자 (h는 0~1까지 모든 실수)
예를 들어 h가 나올 확률이 0.7일 확률은 얼마인지에 대해 묻는다면 이 질문에 대한 확률의 답은 아무리 작더라도 확률값이 매우 많기 때문에 작은 수가 나올 수 없다.

여기서 한 가지 paradox가 있다.
0~1까지 범위 내에 각각의 특정 값은 무한히 셀 수 없고, 0이 아닌 확률이다.
그러므로 확률이 작더라도 각각의 특정 값에 대한 확률을 모두 합하면, 결과적으로 무한한 값이 된다.

반면에 이 모든 확률이 0이라면, 그 확률의 합은 0이 될 것이고,
어떤 하나의 값을 가져야 한다면, 이 값 중 하나일 확률은 1이어야 한다.
이 확률 값이 모두 0이 아닐 수도 있고 모두 0일 수도 있다면, 우리는 무엇을 해야할까?
이것이 바로 pardox이다.
이 paradox를 풀기 위해선 연속 값에 대한 확률로 보는 방법을 배워야한다.
이 방법의 핵심은 각각의 개별 값의 확률을 보는 것이 아니라 값의 범위에 대한 확률을 보는 것이다.
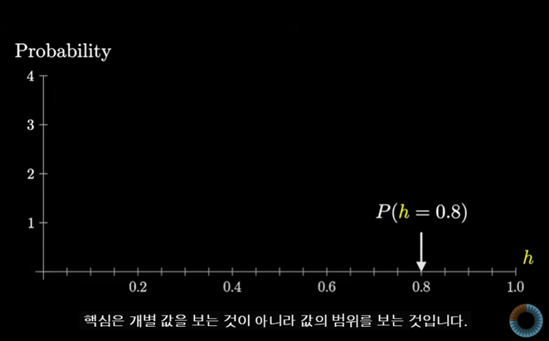
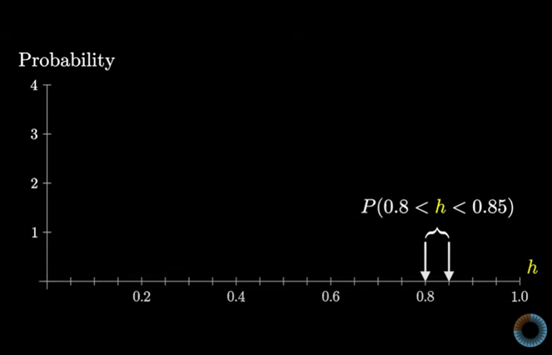
이 범위에 대한 값이 확률을 나타내도록 만들어 볼 수 있다.
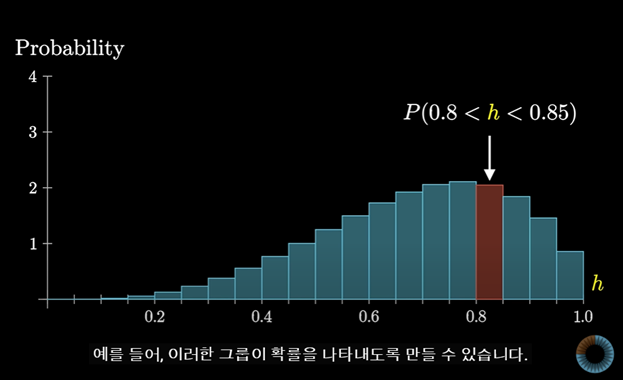
h가 0.8~0.85 사이에 있다고 해보자
막대의 높이가 확률을 나타낸다고 생각하는 대신, 각각의 면적이 확률을 나타낸다고 생각해보자
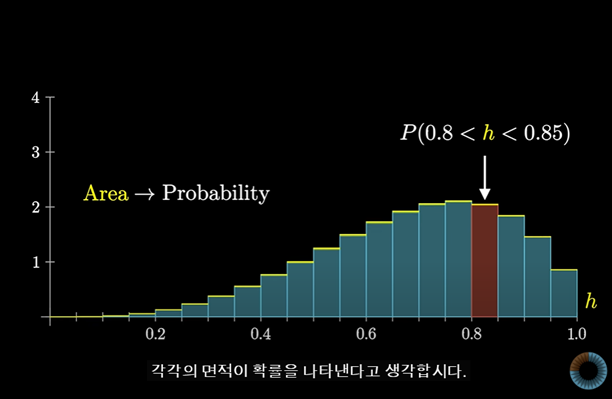
"h"가 이 범위 중 한 곳에 속할 확률에 대한 답을 구하는 것이 우리의 목적이다.
그렇게 하려면 분포를 보다 정확하게 이해해야하고 이 그래프에서의 막대의 면적을 더 잘게 쪼개서 생각해봐야한다.
중요한 것은 이 막대를 쪼개면 쪼갤수록 점점 작은 두께를 가지게 되고 높이는 동일하게 유지된다는 것이다.
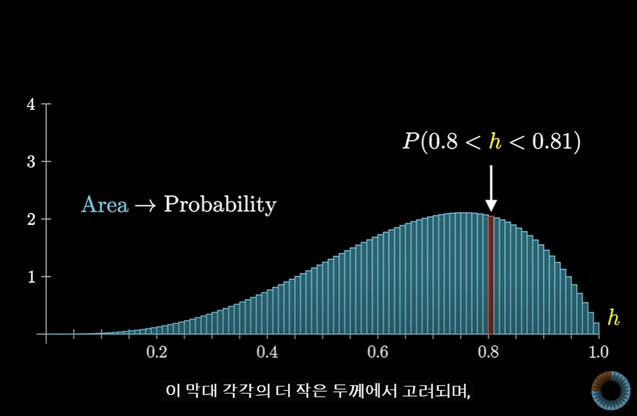
이 과정이 계속해서 이어져 나가면 한계점에서 곡선 형태의 그래프를 얻게 된다.
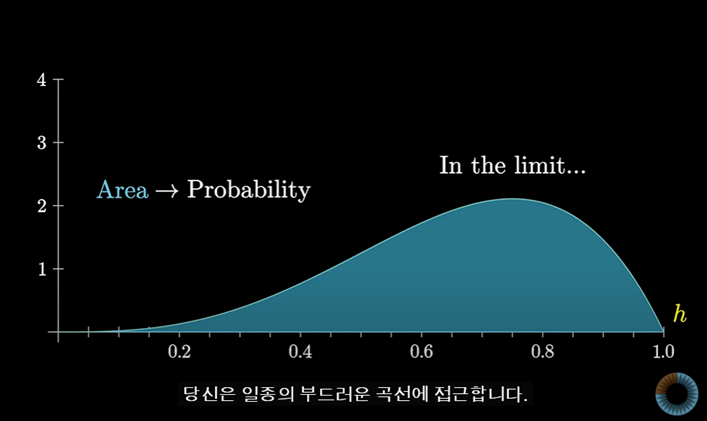
따라서 특정 그룹에 속하는 개별 확률이 0에 가까워지더라도 한계점에서도 분포의 일반적인 모양은 유지된다.
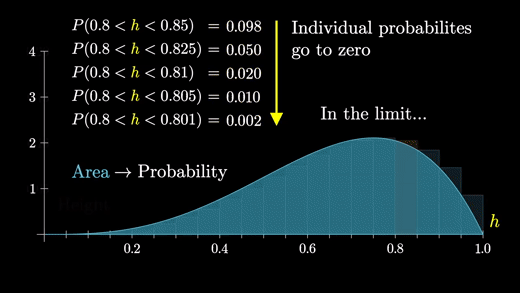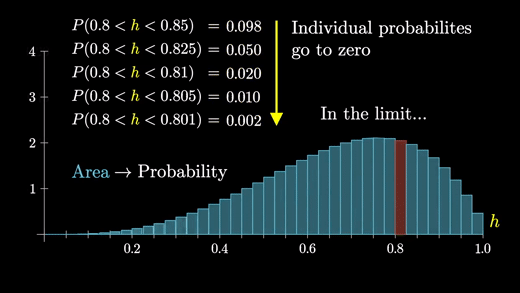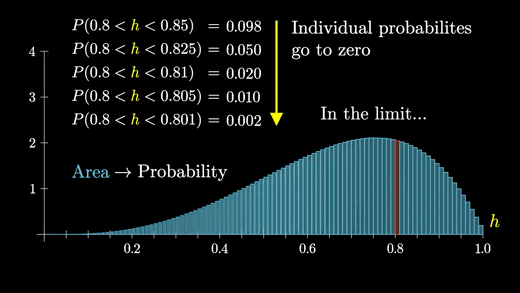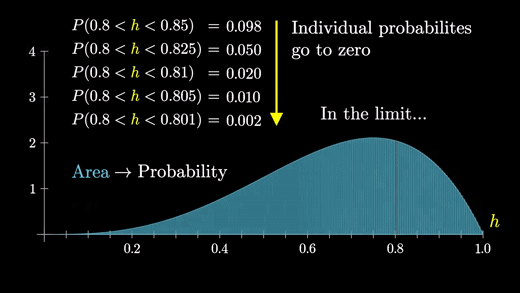
반면에 막대의 높이가 확률을 나타내는 경우, 모든 것은 0이 되었을 것이다.
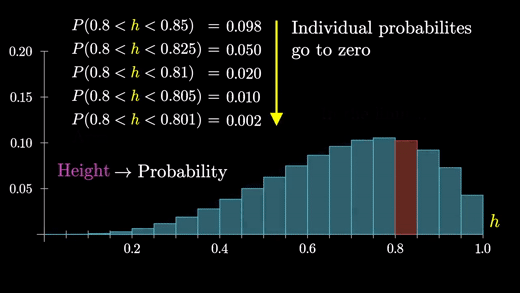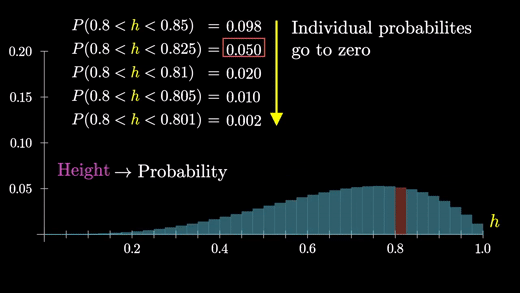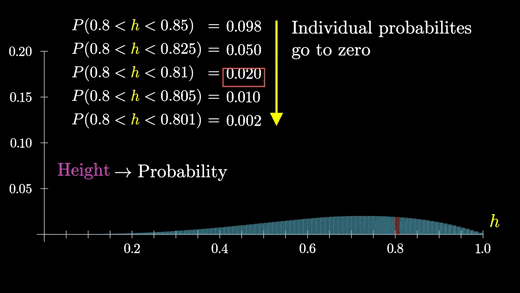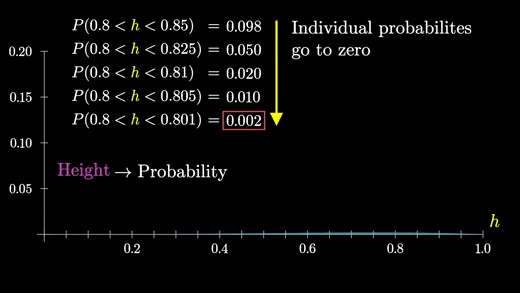
따라서 한계점에서는 분포에 대한 정보가 없는 평평한 선을 가질 것이다.
그러므로 면적을 사용해서 확률을 나타내는 것이 문제를 해결하는 데 도움을 준다.
하지만 y축이 더 이상 확률을 나타내지 않는다면, 이 부분에서의 y축은 무엇일까?
확률은 (h의 범위) x (높이), 즉 막대의 넓이 이므로 높이(y)는 단위 x 범위 당 확률의 값을 나타내며
이를 확률 밀도(probability density)라고 한다.
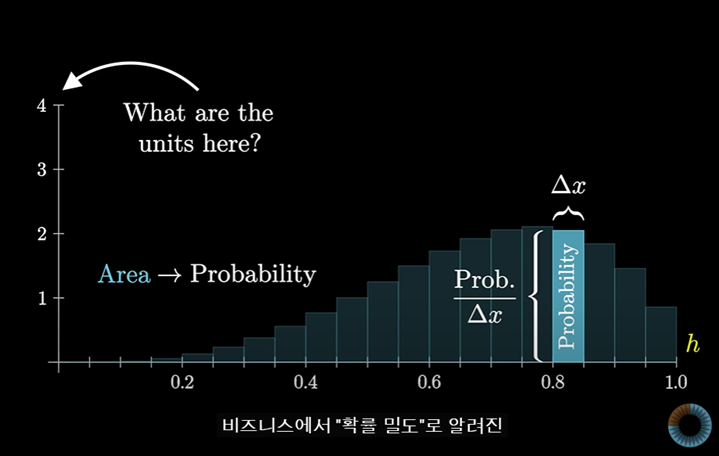
또한 이 막대의 전체 면적은 1이다.
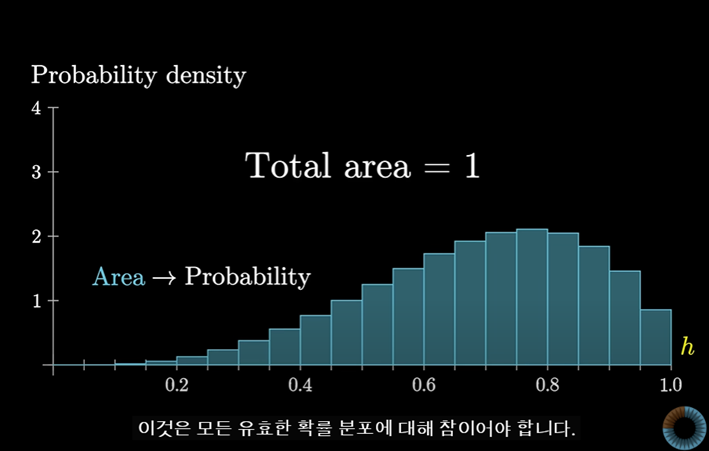
이렇게 막대를 쪼개는 과정을 극한으로 보내게 된다면 0과 1사이에서 셀 수 없는 각각의 무한 값에 확률 밀도를 연결 짓는 데 문제가 없게된다.
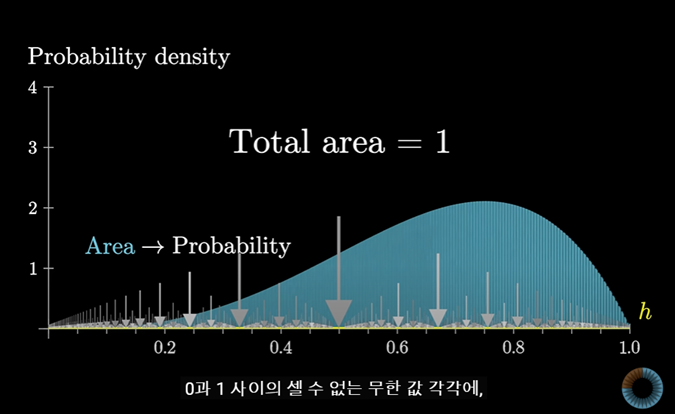
이러한 과정으로 확률밀도함수(PDF)를 만들어 낸다.
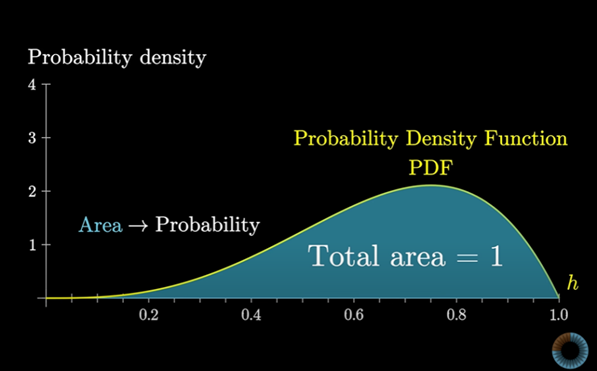
PDF가 관찰될 때마다. 확률 변수를 두 값 사이에 들어갈 확률로 해석해야한다.
이는 두 값 사이에서의 곡선의 아래의 면적과 같다.
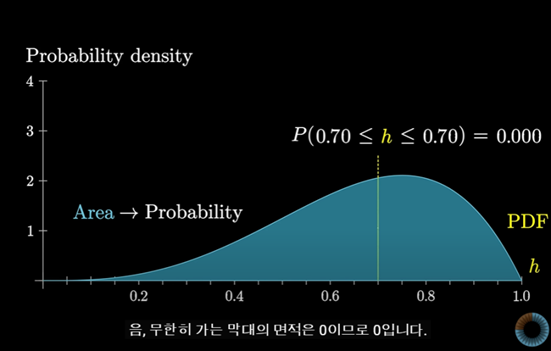
그렇다면 h가 0.7일 확률이 나올 확률은 얼마일까?(특정 숫자가 나올 확률)
무한히 가는 막대의 면적은 0이기 때문에 0이다.
이것들이 모두 합쳐질 확률은 전체 곡선의 아래의 면적이기 때문에 1이 된다.
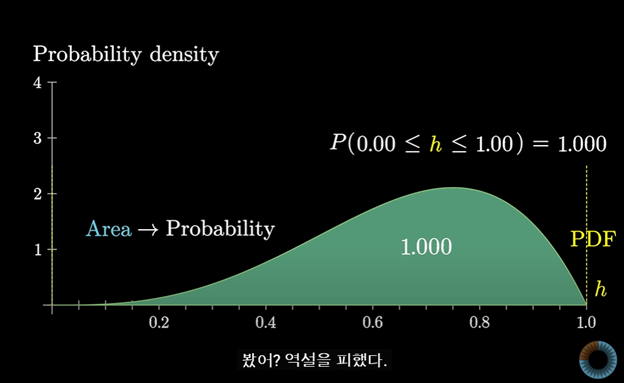
이것이 역설을 푸는 방법이다.
역설을 피하는 방법은 미묘하다.
주사위를 굴리거나 카드를 뽑는 것과 같은 유한적인 일반 경우에서 임의의 값의 가능성에 속할 확률은 단순히 그것들 중 하나일 확률의 합이다.

이것은 무한적인 경우에서도 마찬가지이다.
그러나 이 경우 연속적인 확률이기 때문에 규칙이 변경된다.
범위에 속할 확률을 생각해야하기 때문이다. 더 이상 각 개별 값의 확률의 합이 아니다.
대신 값의 범위에 대한 확률을 하나의 개체로 보는 것이다.

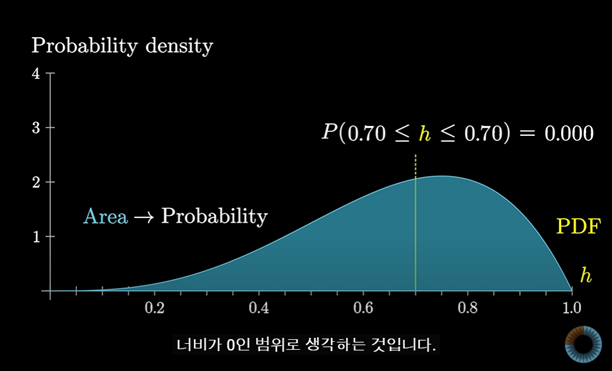
discrete context와 contiunous context 사이에서 규칙이 변경된다는 생각이 어렵다면, 측정 이론을 생각해보자.
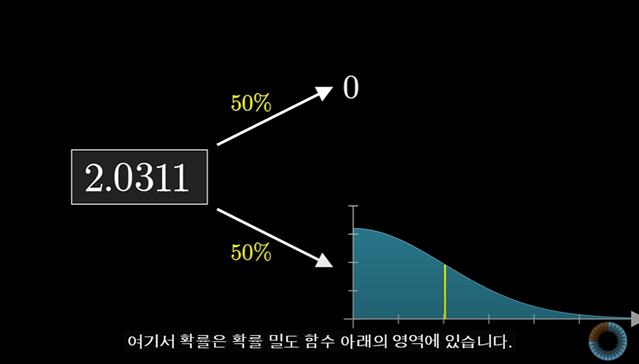
예를 들어 임의의 값이 0이 나올 확률은 50%이며, 양수가 나올 확률도 50%인 경우를 생각해보자
정규곡선의 절반처럼 보이는 분포에 따라 이것은 무한함과 유한함 사이의 중간지점으로 볼 수 있다.
어떤 확률값이 0이 아닌 경우에는 이 때의 확률은 확률밀도함수영역에 있게 된다.
Discrete context에서는 일반적인 법칙으로 확률의 합을 사용하지만
Contionuous context에서는 적분을 사용한다. 이는 곡선 아래의 면적을 찾는 데 사용하는 도구이다.

다시 동전던지기의 상황으로 돌아가보자
배운 내용을 바탕으로 우리가 앞의 상황에 대해서 다시 질문해본다면
몇 번의 결과값을 본 후 “h”를 설명하는 확률밀도함수는 무엇입니까? 로 해석할 수 있다.
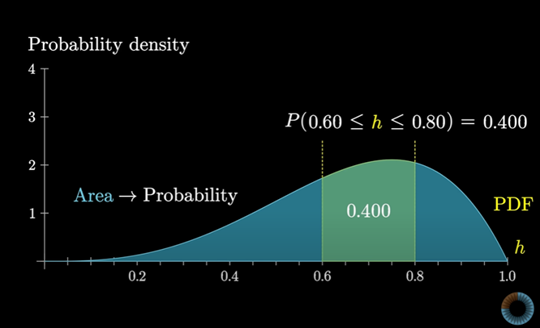
해당 PDF를 찾은 경우 “실제로 앞면이 나올 확률이 0.6에서 0.8사이에 있다면 그 확률은 얼마입니까?”에 대한 질문을 답하는 데 사용할 수 있다.
이에 대한 답을 얻어내는 과정은 다음 시간에 학습한다.
- 확률밀도함수?
- 연속확률변수 x에 대한 f(x) --> 확률밀도함수는 확률이 아니다!
'수학 > 확률론' 카테고리의 다른 글
| [3Blue1Brown] Part 4 | The quick proof of Bayes' theorem (0) | 2022.08.15 |
|---|---|
| [3Blue1Brown] Part 3 | Bayes theorem, the geometry of changing beliefs (0) | 2022.08.15 |
| [3Blue1Brown] Part 1 | 수학적으로 어느 별점이 더 나은 걸까? (0) | 2022.08.09 |
