{학습 목적}
part 3에서는 베이즈 이론에 대해서 학습한다.
이 부분을 학습하는 이유는 베이즈 정리가 불확실성 상황에서 의사결정을 내리는데 중요하게 사용되기 때문이라고 생각된다.
즉, 베이즈 정리는 데이터가 주어지기 전의 사전 확률값이 데이터가 주어지면 어떻게 변하는지 사후 확률을 통해 알 수 있다.
<베이즈 이론>
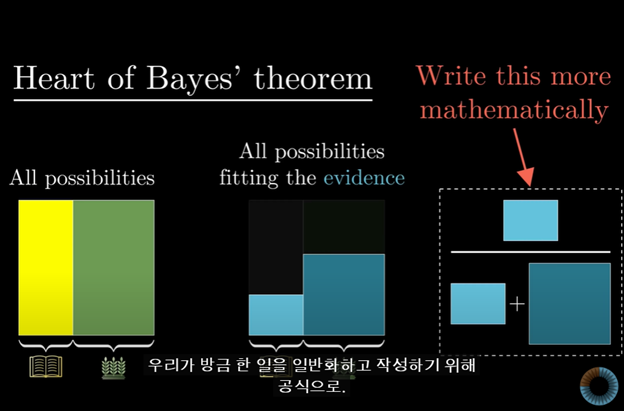
베이즈 정리에 대해서 3가지 단계를 통해 이해해볼 수 있다.
1. 공식의 각각 개별부분의 의미를 이해해본다.
2. 그리고 다이어그램을 통해 그 공식이 참인 이유를 알아본다.
3. 마지막으로 이 공식을 언제 사용하는지 이해해보는 것이다. (가장 중요)
이 강의에서는 3단계를 역순으로 살펴보고 있다.
공식을 언제 사용하는지에 대해 이해해보기 위해 스티브란 사람의 예시를 들고 있다.
스티브의 성격이 meak and tidy 하다는 증거를 가지고 그가 사서인지 농부인지 예측해보는 확률을 도출해보려한다.
먼저 표본이 되는 200명의 농부와 10명의 사서를 생각해보자
10명의 사서 중 meak and tidy한 사서는 40%, 즉 4명이고
200명의 농부 중 meak and tidy한 농부는 10% 즉 20명이라고 한다면
description(추정치)는 20+4 = 24가 되고
실제 meak and tidy한 사서는 4명이 되어
스티브가 meak and tidy한 사서가 될 확률은 4/24, 즉 16.7%가 된다.
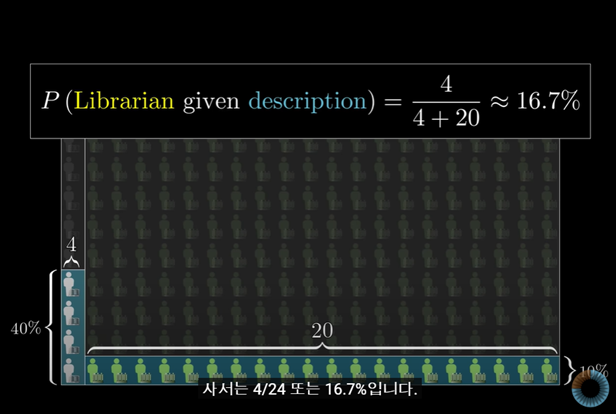
사서일 확률은 40%, 농부일 확률은 10% , 사서일 확률이 더 높다고 하더라도 농부가 더 많은 것은 사실이다.
그러므로 사전확률이 중요하다는 것을 알 수 있다.
이것이 베이즈 정리의 핵심이다.
그렇다면 언제 베이즈 정리를 사용할 수 있을까?
스티브가 사서라고 가정해보자. 그리고 스티브는 meak and tidy하다는 증거가 주어져있다.
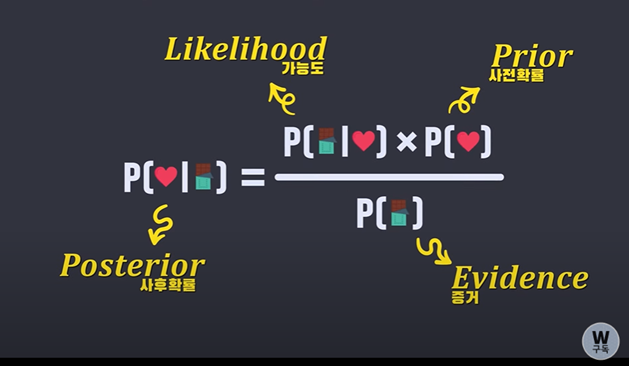
전체 표본 중 사서일 확률은 1/21이라는 "Prior"(사전확률)이 주어져있다.
그리고 우리는 사서들 중 meak and tidy인 사람들의 확률이 0.4이라는 것을 알고있다.
베이즈 정리에서는 이 확률을 "likelihood(가능도)"라고 부른다.

마찬가지로 사서가 아닌 농부 중 meak and tidy한 농부일 확률은 0.1인 것을 알고있다.
이 때 사서가 아니라는 not 기호를 쓴다.
이제 주어진 증거에 대해서 스티브가 사서라는 가설이 맞을 확률에 대해서 생각해보자
분자에는 meak and tidy한 사서의 인원 수인 4가 오게 될 것이다.
그리고 분모에는 meak and tidy한 총 인원수 24명이다.
4는 어디서 올까?
이는 총 인원 수에서 이전 확률(P(H))인 1/21을 곱한 값이다.
그리고 likelihood (P(E|H))를 곱해줘야한다. --> 210*1/21*4/10 = 4
분모는 분자의 값에 총 인원수에서 농부의 확률를 곱하고 농부들 중 meak and tidy한 농부일 확률을 곱하면 된다.
--> 4 + (210*20/21*1/10) =24
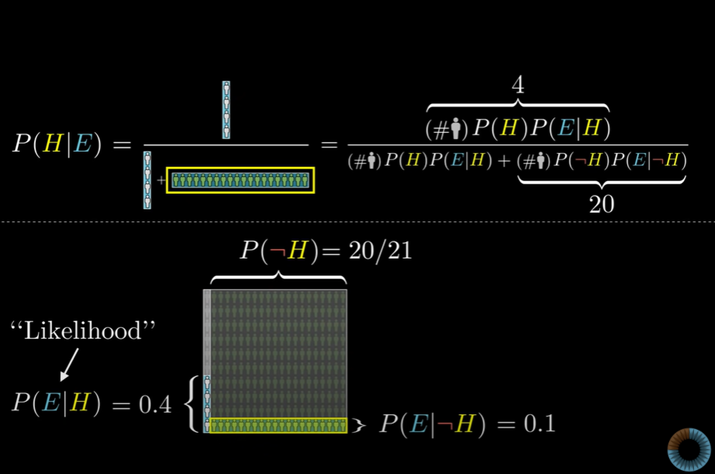
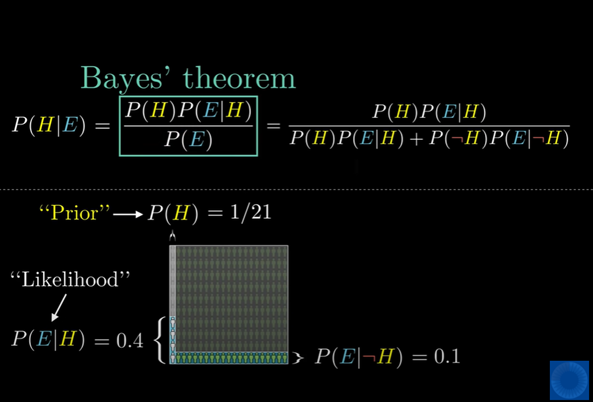
P(H|E)와 같은 확률을 “Posterior”(사후확률)이라고 부른다.
+ 베이즈 정리를 정사각형을 통해 이해하는 방법
(출처: 유튜브 위니버스 채널, 베이즈 정리를 이해하는 가장 쉬운 방법)
우리가 원하는 확률은 초콜릿을 주었을 때 상대방이 나를 좋아하게 될 확률이다.
여기서 사전확률은 상대방이 나를 좋아할 확률 0.5 좋아하지 않을 확률 0.5라고 가정한다.
베이즈 정리를 쉽게 이해하는 방법은 상황을 넓이가 1인 정사각형으로 시각화 하는 것이다.
즉 사각형의 넓이는 전체확률 100%를 나타낸다.
여기서 상대방이 나를 좋아하거나 좋아하지 않을 확률을 사각형의 가로길이로 생각한다.
따라서 사전확률로 설정했던 상대방이 날 좋아할 확률 0.5는 사각형의 왼쪽 절반 넓이로 표현될 수 있다.
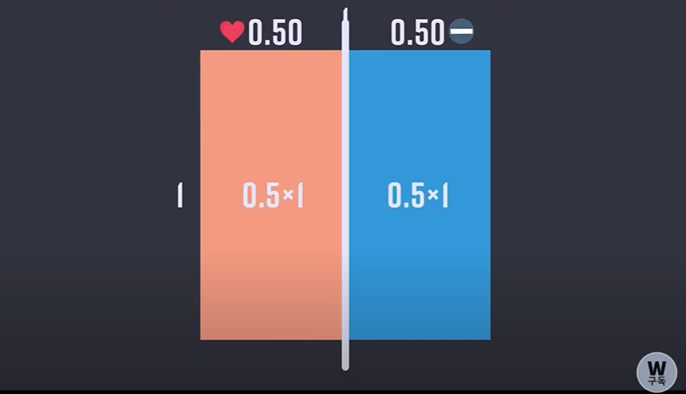
사각형의 세로 길이는 상대방이 나를 좋아하거나 좋아하지 않을 때 초콜릿을 줄 확률이다.
좋아하는 사람일 경우 초콜릿을 줄 확률은 0.4이기 때문에 왼쪽 위의 사각형의 넓이는 0.2이이다.
좋아하는 사람인데도 초콜릿을 주지 않을 확률은 0.6이므로 왼쪽 밑의 사각형의 넓이는 0.3이다.
좋아하지 않는 사람일 때 초콜릿을 줄 확률은 0.3이므로 오른쪽 위의 넓이는 0.15,
오른쪽 아래의 직사각형은 0.35이다.
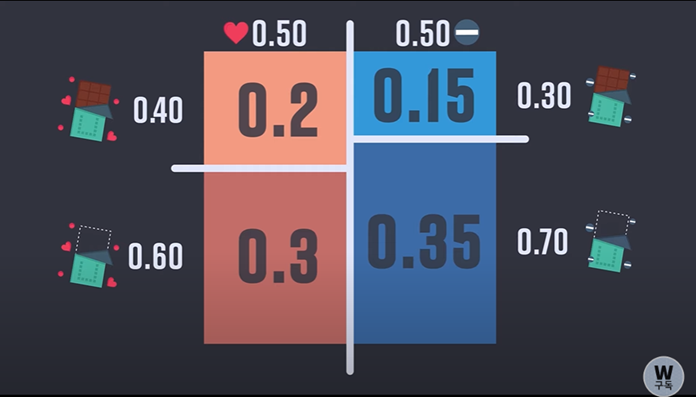
이 작은 정사각형 넓이 자체가 확률이 되고 이 확률을 다 더하면 1이 된다.
우리는 이제 초콜릿을 받은 관찰영역만 보면 된다.
초콜릿을 받은 영역을 분모로 하고 호감이 있으면서 초콜릿을 받은 영역을 분자로 해서 사후확률 0.57를 구할 수 있다.
베이즈 정리는 데이터가 많을수록 올바른 의사결정을 내릴 확률이 높아진다.
사전확률을 지속적으로 업데이트 하는 것이 베이즈 정리의 중요한 통찰이다.
- 베이즈 정리?
- 사전확률과 사후확률 사이의 관계를 나타내는 정리
'수학 > 확률론' 카테고리의 다른 글
| [3Blue1Brown] Part 4 | The quick proof of Bayes' theorem (0) | 2022.08.15 |
|---|---|
| [3Blue1Brown] Part 2 | Why “probability of 0” does not mean “impossible” (0) | 2022.08.11 |
| [3Blue1Brown] Part 1 | 수학적으로 어느 별점이 더 나은 걸까? (0) | 2022.08.09 |
