{학습 목적}
Part 4에서는 베이즈 정리를 수학적 관점에서 보는 것에 대해서 설명한다.
이 부분을 학습하는 이유는 베이즈 공식에 대해서 빠르게 이해하고 어떤 상황에 적용해볼 수 있는지 알아보기 위해서라고 생각한다.
A,B 두 사건이 있다고 가정해보자
이 사건 두 개가 동시에 일어날 확률은 어떻게 될까?
이는 (모든 사건에 대해서 A가 일어날 확률) x( A가 일어난다고 가정했을 때의 B가 발생할 확률)의 공식을 이용하면 된다.
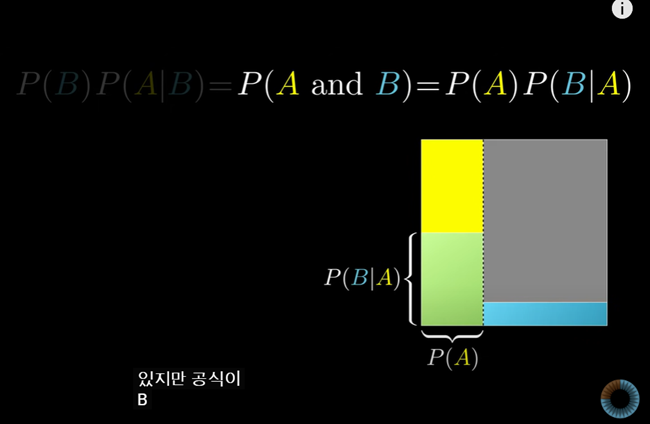
이는 (모든 사건에 대해서 B가 일어날 확률) x (B가 일어난다고 가정했을 때의 A가 발생할 확률)의 공식을 이용한 것과도 같다.
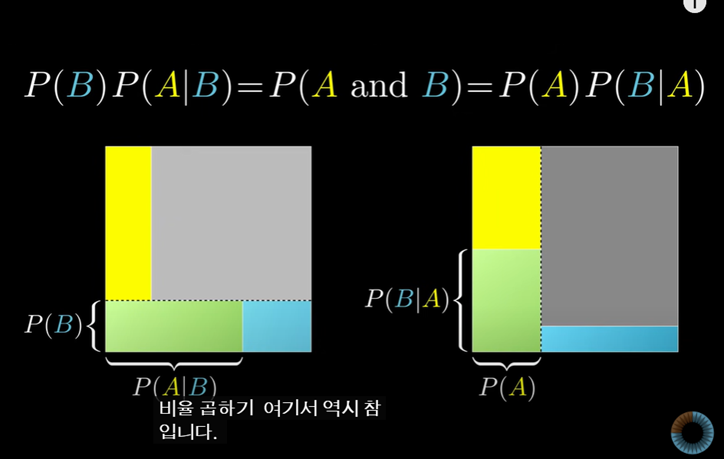
이 공식은 다음과 같이 표현할 수 있다.


이 공식을 더 빠르게 이해할 수 있는 방법에 대해서 알아보자
A와 B가 동시에 일어날 확률이 A와B의 각각의 확률을 곱한 것이 아니라는 사실을 아는 것이 중요하다.
예를 들어 4명 중 1명이 심장병으로 사망했다고 했을 때, 형제가 사망할 확률은 1/4 *1/4 = 1/16일까?

동전던지기의 상황과 비교해보자
동전던지기에서 연속해서 두 번 모두 뒷면이 나올 확률은 1/2*1/2 = 1/4이다.
이는 심장병으로 사망하는 경우와는 다르다.
형제가 심장병으로 인해 사망한 경우에는 유전, 생활방식의 영향이 있을 수도 있기 때문이다.
그러므로 심장병으로 사망할 확률에는 어떠한 가정을 전제 하에 두어서 구해야한다.
하지만 동전던지기나 두 개의 주사위를 던지는 경우에는 각 사건이 서로 무관하므로 앞에서 나온 사건을 고려하지 않고 두 사건을 그냥 곱해주면 된다.
이것이 독립의 정의라고 할 수 있다.

즉, 베이즈 정리는 하나의 변수가 다른 변수에 얼마나 의존하는 지 측정하는 데 유용하다.
'수학 > 확률론' 카테고리의 다른 글
| [3Blue1Brown] Part 3 | Bayes theorem, the geometry of changing beliefs (0) | 2022.08.15 |
|---|---|
| [3Blue1Brown] Part 2 | Why “probability of 0” does not mean “impossible” (0) | 2022.08.11 |
| [3Blue1Brown] Part 1 | 수학적으로 어느 별점이 더 나은 걸까? (0) | 2022.08.09 |
