{학습 목적}
Chapter 7에서는 역행렬, 계수, 열공간, 영공간에 대해서 다룬다.
이 개념을 학습하는 이유는 복잡한 방정식계를 공간의 변형, 벡터의 움직임과 역행렬, 열공간, 영공간을 사용하여 해를 구할 수 있게 해주는 선형대수의 유용성에 대해 알아보기 위해서라고 생각한다.
<역행렬, 열공간, 영공간>
방정식계(system of equations): 미지수인 변수 리스트와 변수들과 관련된 방정식을 가진 것

각 방정식 내에서, 각 변수들의 역할은 어떤 상수를 스케일링 하는 것이다.
그리고 스케일 된 변수들을 서로 더하는 게 전부이다.
이런 변수들을 조직화 한 것이 특수한 방정식계이다.

모든 변수들을 좌항으로 보내고 오른쪽에는 상수항을 놓는다. 이렇게 놓는 것을 선형방정식계(linear system of equations)라고 한다.
모든 방정식들을 하나의 벡터 방정식으로도 표현할 수 있다.
상수계수만을 모아서 행렬을 만들고, 변수들을 모아서 벡터를 만들어서 행렬 벡터 곱셈하면 어떠한 상수 벡터와 같아지게 된다.
행렬 A는 어떤 선형변환을 나타내고, Ax =v는 변환 후에 벡터 v가 되는 벡터 x가 있는지 찾아보는 것이다.
즉, 여러 변수들이 있는 선형 방정식을 공간을 변형시키는 것으로 생각하고, 벡터가 어디로 이동하는지 찾으면 되는 것이다.
2x2 행렬에서 방정식의 해를 찾는 방법은 행렬 A 변환이 모든 공간을 더 낮은 차원으로 축소시키는지(선이나 점), 그대로인 지를 알아보는 것이 우선이다.
행렬식의 개념을 도입하면 행렬 A의 행렬식 값이 0인지, 0이 아닌지로 나누는 것과 같다.
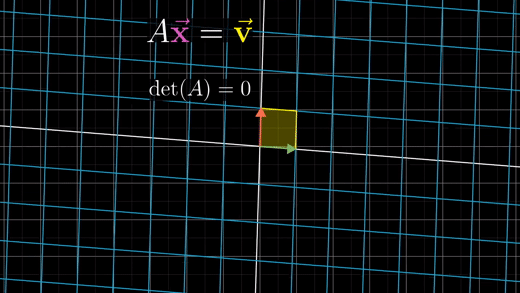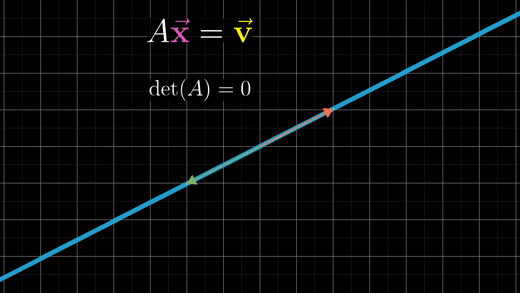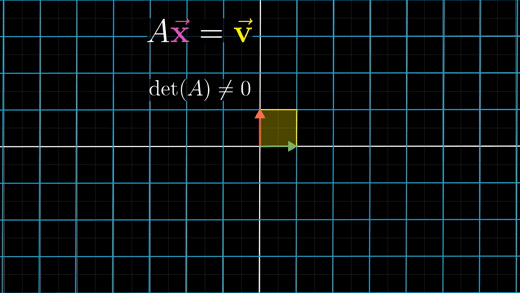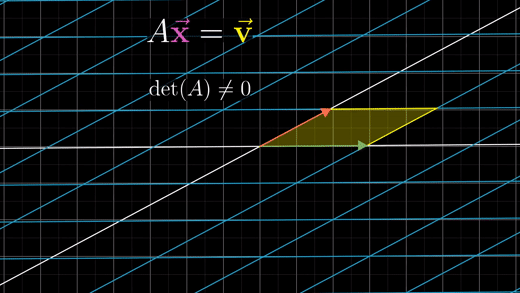
- 행렬식 값이 0이 아닌 경우 (= 공간을 제로 영역으로 축소시키지 않는 경우)
특정 v벡터로 변할 수 있는 벡터는 항상 하나이다. (일대일 대응 변환)
v 벡터에서 x벡터로 변환을 역방향으로 돌리면 벡터 x를 찾을 수 있다.
이 때, 역으로 변환하는 것을 A의 역행렬(Inverse matrices) 이라고 한다.
A의 윗첨자로 -1을 써서 표기한다.
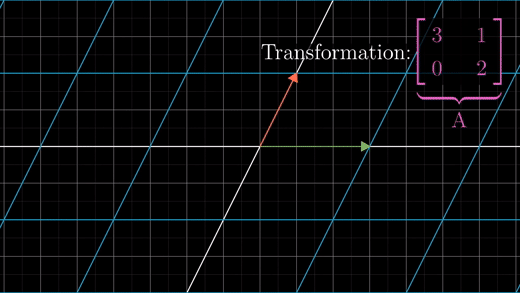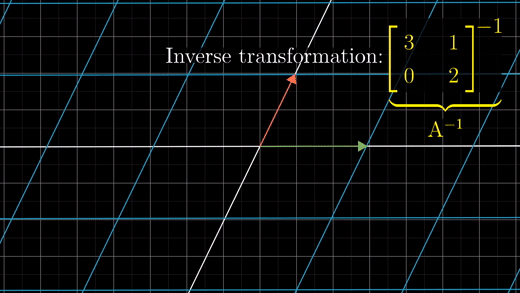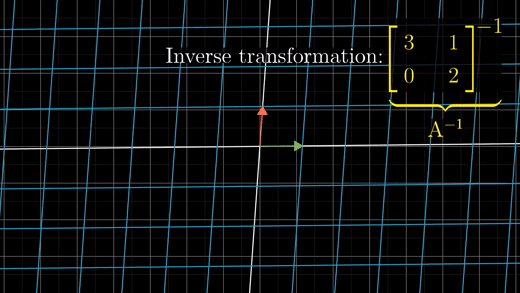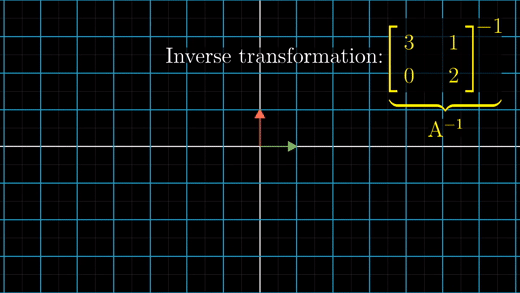
A 역행렬의 특별한 속성은 A행렬을 적용한 뒤, A 역행렬을 적용하면, 다시 시작한 점으로 돌아오게 된다는 것이다.
이렇게 연달아 적용하는 변환을 행렬 곱셈으로 대수적 축약할 수 있다.
즉 A역행렬 변환이 가진 핵심 속성은 A역행렬*A행렬은 아무것도 바꾸지 않는 행렬과 같다는 것이다.
아무것도 변하지 않는 변환을 항등변환(identity transformation)이라고 한다.
i-hat과 j-hat이 이동하지 않고 그대로이기 때문에 각각 (1,0)(0,1)을 가르키게 된다.

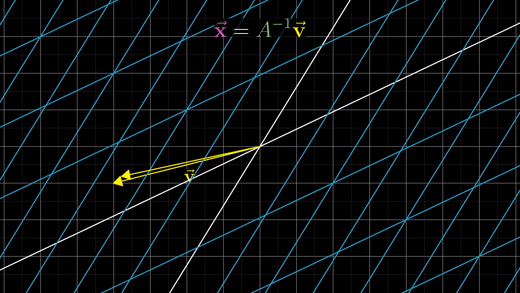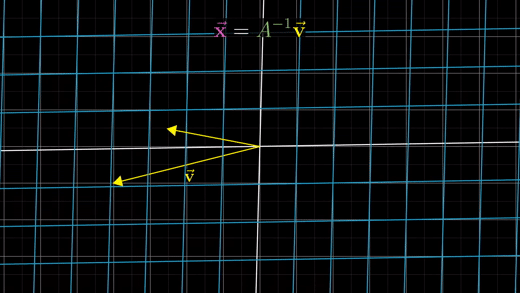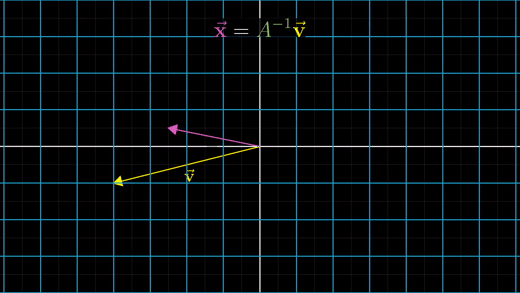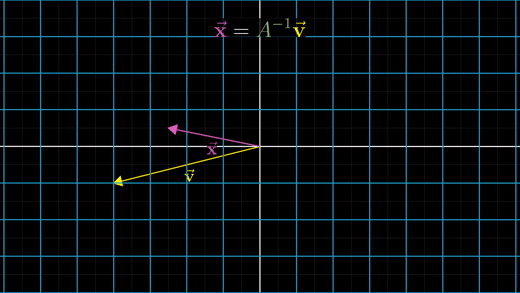
역행렬을 찾은 후에는 Ax벡터 = v벡터 방정식에 역행렬을 v벡터에 곱해서 풀 수 있다.
기하학적으로 보자면, 이것은 v벡터에 역변환을 가한 것을 의미한다.
*3차원에서의 역행렬
3차원의 경우에도 마찬가지로 미지수 개수와 방정식 개수가 같다면 방정식계는 기하학적으로 어떤 변환을 나타내는 A행렬과 벡터 v를 가지고 벡터 v로 변환되는 x를 찾는 것이 된다.
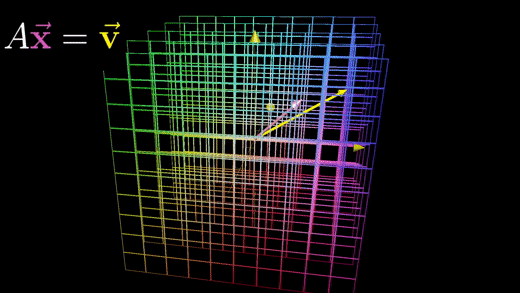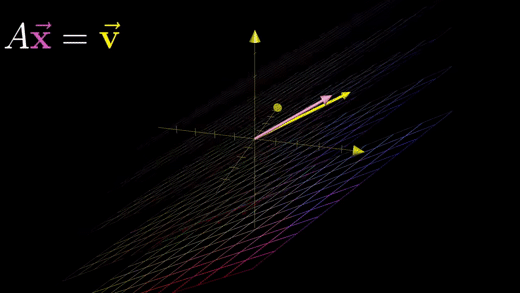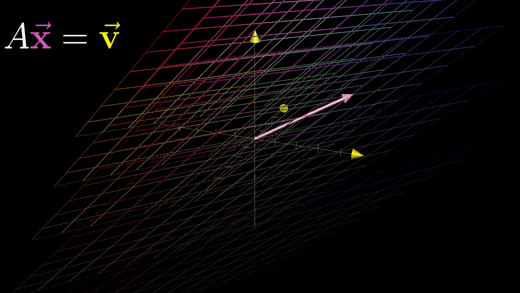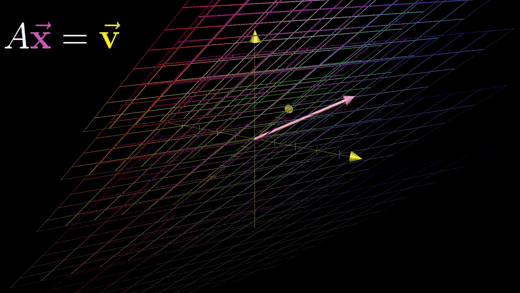
변환 A가 공간을 더 낮은 차원으로 뭉게지지 않는 한, 즉 행렬식 값이 0이 아닌 경우, 역행렬 A가 존재하게 된다.
마찬가지로 이 역행렬 변환도 항등 변환이다.
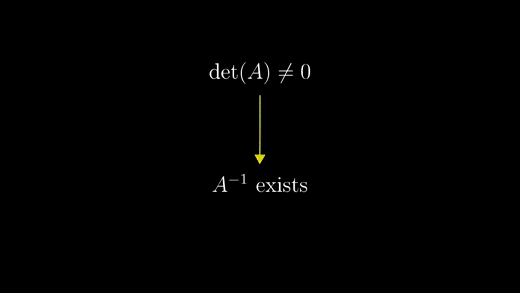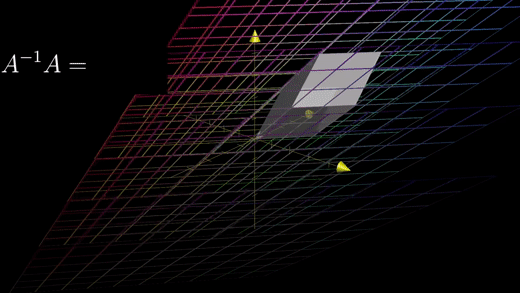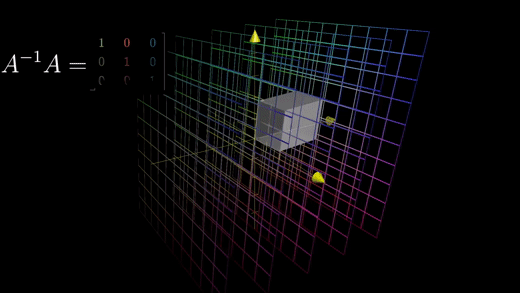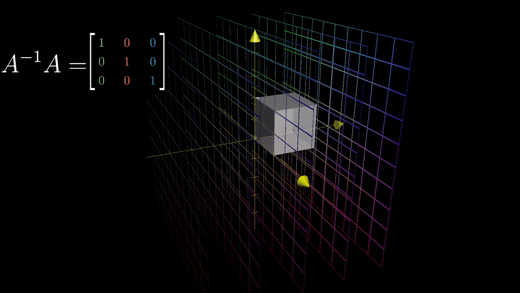
2. 행렬식 값이 0인 경우
역행렬은 존재하지 않게 된다.
뭉게진 선을 되돌려서 평면으로 만들 수 없다. 그것은 함수의 기능에 부합하지 않는다.
이것을 가능하게 하려면 각 벡터를 변환시켜서 하나의 온전한 선, 선을 이루는 모든 벡터로 바꿔야한다.
하지만 함수들은 하나의 입력을 받아 하나의 출력만 만들기 때문에 이것은 불가능하다.
하지만 역행렬이 없는 경우에도 해는 여전히 존재할 수는 있다.
어떤 변환이 공간을 하나의 선으로 변환시키는 경우라면, 벡터 v가 그 선 위에 놓여있는 경우에만 해를 구할 수 있다.

[계수]
3차원 공간에서와 같이 행렬식이 모두 0이어도 공간을 선으로 축소하는 경우가 공간을 평면으로 축소하는 경우보다 해가 존재하기 어려운 경우가 있기 때문에 계수라는 개념을 도입한다.
계수(rank): 변환 결과(열공간)의 차원의 수
변환의 결과가 선이라면, 즉 1차원 이라면, 이 경우 랭크 1(rank=1)이라고 한다.
변환 후 모든 벡터가 2차원 공간에 놓여있다면, 이때는 랭크 2(rank=2)라고 한다.
예를 들어 2x2 행렬의 경우에, 최대로 될 수 있는 rank는 2이다.
이는 기저벡터들을 확장시켜 온전한 2차원 공간을 만들 수 있다는 것이다.
[열공간]
열공간(column space): 행렬의 열들의 확장 공간(span)이다.
3x3 행렬에서, rank가 2라는 말은 공간이 축소했음을 의미한다.
3차원 변환의 행렬식 값이 0이 아니면서 3차원 공간의 결과가 온전한 3차원이라면, 이 때는 rank는 3이다.
행렬의 열들의 가능한 결과의 집합(선이든 평면이든 3차원 공간이든지)을 그 행렬의 “열공간(column space)”라고 부른다.
행렬의 열들은 기저 벡터의 변환 후 위치이고, 이 변환 후 기저벡터들의 확장공간은 가능한 모든 결과공간을 알려준다.
이 rank가 높아질수록 열의 개수와 같다는 말이고, 이 때를 온전한 랭크(full rank)라고 부른다.
[영공간]
영벡터는 어느 열공간에든지 포함되어있다.
선형변환은 반드시 원점이 고정되어있어야 하기 때문이다.
영공간(null space), 커널(kernel): 원점으로 이동되는 벡터들의 집합, null이 되는 모든 벡터의 공간, 벡터들 모두 영벡터가 된다는 의미
선형방정식계 용어로 말하면, A행렬*x벡터 = v벡터 방정식에서 벡터v가 영벡터인 경우, 영공간(null space)모두가 해가 될 수 있다.
- 역행렬?
- 변환된 어떤 벡터를 원상복구해주는 변환
- 계수?
- 기저 벡터의 변환 후 공간 차원 수
- 열공간?
- 기저 벡터의 변환 후 확장 공간
- 영공간?
- 영벡터로 이동하는 벡터들의 집합이 이루는 확장 공간
'수학 > 선형대수학' 카테고리의 다른 글
| [3Blue1Brown] Chapter 9 | Dot products and duality (0) | 2022.08.02 |
|---|---|
| [3Blue1Brown] Chapter 8 | Nonsquare matrices as transformations between dimensions (0) | 2022.07.30 |
| [3Blue1Brown] Chapter 6 | The determinant (0) | 2022.07.30 |
| [3Blue1Brown]Chapter 5 | Three-dimensional linear transformations (0) | 2022.07.29 |
| [3Blue1Brown]Chapter 4 | Matrix multiplication as composition (0) | 2022.07.29 |
