{학습 목적}
Chapter 5에서는 앞에서 배웠던 선형변환을 3차원 공간에 적용해본다.
이 부분을 학습하는 이유는 변환이 입력 벡터를 *움직여서* 출력 벡터를 만든다는 컨셉을 다시 한번 상기시켜 3차원 공간에서의 선형변환을 이해해보기 위해서라고 생각한다.
즉, 수치적 표현보다는 시각적 표현으로 개념을 이해하여 3차원 공간으로의 개념 확장을 보여주고 있는 것 같다.
<3차원에서의 선형변환>
3차원에서의 선형변환도 2차원과 마찬가지로 기저 벡터의 움직임을 알면 완벽하게 알아낼 수 있다.
이 때 기저 벡터로 z축이 추가되는데 z축의 단위 벡터는 k-hat이라고한다.
어떤 벡터 [x,y,z]가 변환 후 어디가 되는 지는 2차원에서 했던 방법과 동일하다.
각 좌표 값을 스케일링 팩터로 보면 된다.
각 기저 벡터들을 그 팩터로 스케일링해서 합치면 원하는 결과 벡터를 얻게 된다.
중요한 점은 이렇게 스케일링과 더하는 절차가 변환 전-후에도 같다는 것이다.
그래서 벡터의 변환 결과를 알려면, 벡터의 좌표값을 행렬에 대응되는 열과 곱한 다음 그 결과들을 합하면 된다.
Q) 3x3행렬끼리의 수치적으로 행렬곱셈은 어떻게 풀어나갈까?
공간 속에서 연속된 변환의 적용에 대한 아이디어를 생각해보면서 이 곱셈을 어떻게 수행할 지 생각해보자.
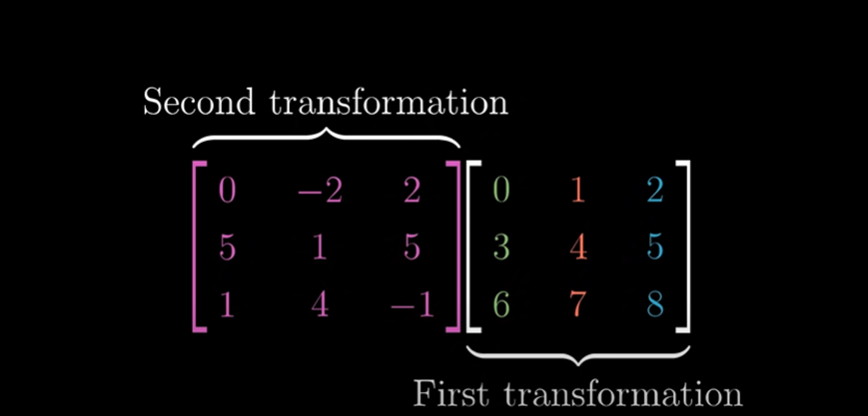
A) 첫 번째로 변환된 i-hat을 왼쪽 행렬에 곱하여 두 번 변환된 최종 위치의 벡터를 구할 수 있다.
마찬가지로 변환된 j-hat을 왼쪽 행렬에 곱하여 두 번 변환된 j-hat의 최종 위치의 벡터를 구할 수 있고
k-hat도 이와 같은 방법으로 최종 위치를 구할 수 있게되어 두 선형변환의 합성 결과를 알 수 있다.
'수학 > 선형대수학' 카테고리의 다른 글
| [3Blue1Brown] Chapter 7 | Inverse matrices, column space and null space (0) | 2022.07.30 |
|---|---|
| [3Blue1Brown] Chapter 6 | The determinant (0) | 2022.07.30 |
| [3Blue1Brown]Chapter 4 | Matrix multiplication as composition (0) | 2022.07.29 |
| [3Blue1Brown] Chapter 3 | Linear transformations and matrices (0) | 2022.07.29 |
| [3Blue1Brown] Chapter 2 | Linear combinations, span, and basis, vectors (0) | 2022.07.29 |
