{학습 목적}
Chapter 6에서는 행렬식에 대해 학습한다.
행렬식은 앞 챕터에서의 선형 변환, 즉 공간 변형의 개념을 적용하여 이루어지는 것 같다.
앞에서는 공간의 변형을 다뤘다면 이 부분에서는 기저 벡터가 이루는 단위 영역의 개념으로 축소하여 좀 더 깊이 있게 변형을 이해해보는 과정인 것 같다.
즉, 이 개념을 공부하는 이유는 공간의 변형의 개념을 좀 더 축소화한 단위 영역의 변환을 시각적으로 바라보기 위해서라고 생각한다.
<행렬식>
[행렬식]
행렬식(determinant): 선형 변환에 의한 단위 정사각형의 영역의 변화를 나타내는 팩터
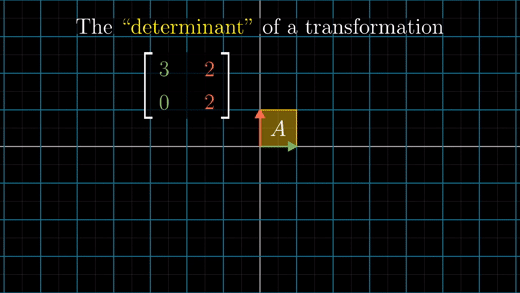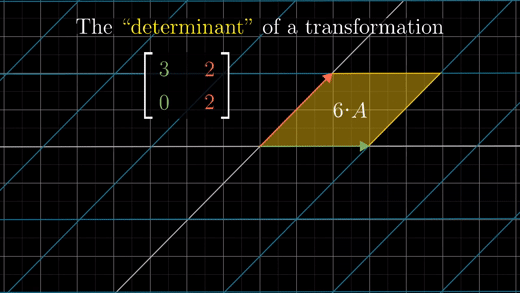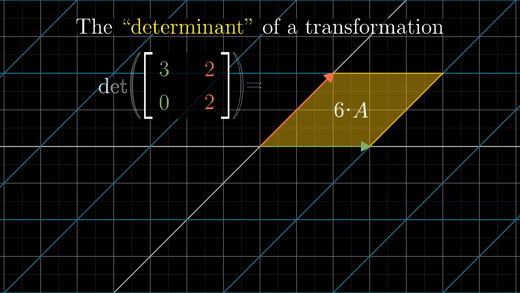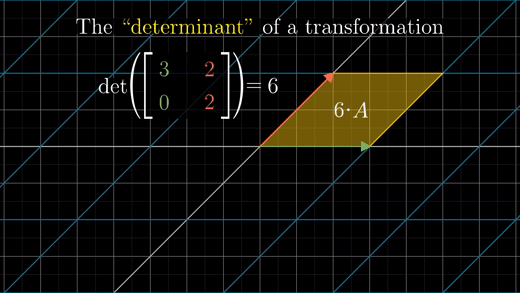
예를 들어 행렬식 값이 6이라면, 영역 크기를 6으로 확장하는 것을 의미한다.
2차원 변환의 행렬식 값이 0이라면, 어느 영역이든 크기가 0이기 때문에 모든 공간이 찌그러져서 선이 되거나 점이 될 수 있다.
행렬식 값이 음수값이라면 공간의 방향(orientation)이 뒤집힌다는 의미이다.
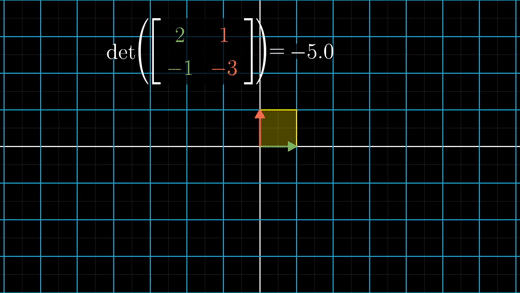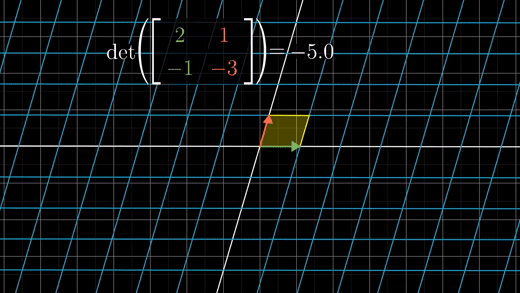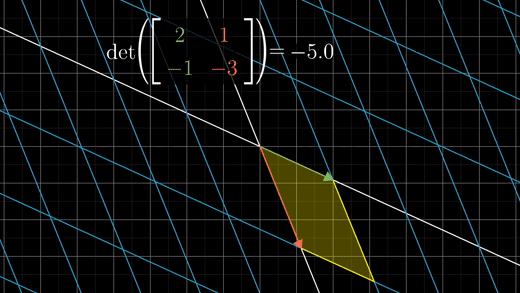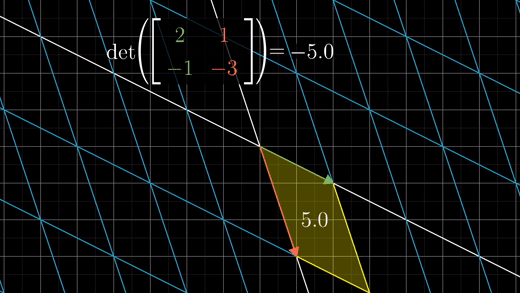
이 행렬식의 절대값을 영역 스케일링에 관한 팩터로 볼 수 있다.
[3차원에서의 행렬식]
3차원인 3x3행렬에서의 행렬식 값은 부피가 얼마나 스케일링 되는지를 알려준다.
3차원 행렬에서는 하나의 1x1x1 정육면체에 집중한다.
변환 후 이 정육면체는 기울어진 정육면체가 되는데 이를 평행육면체(parallelepiped)이라고 한다.
즉, 행렬식의 값은 부피 1인 정육면체가 바뀐 후의 평행육면체의 부피를 알려주는 것이다.
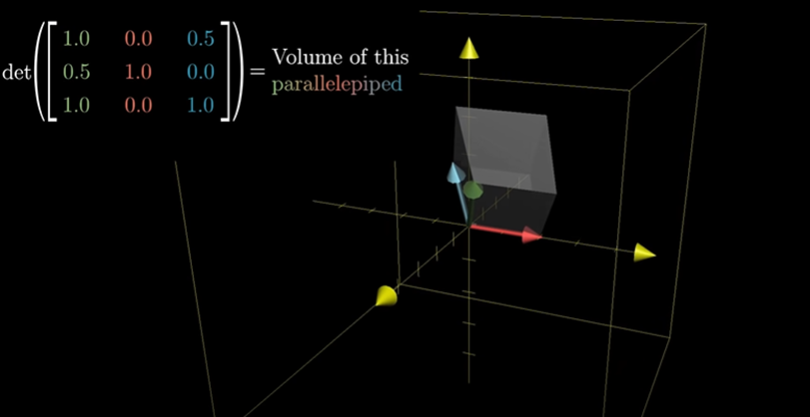
+ 앞에서 배웠던 선형 종속의 개념을 생각해보면, 행렬식이 0이라는 것은 공간이 찌그러져서 선이나, 점을 만들기 때문에 벡터들 중 하나가 다른 벡터들의 span에 포함되는 경우이다.
그러므로 그 행렬의 열들이 선형종속(lineary dependent)하다고 할 수 있다.
3차원에서 행렬식의 음수 값이 의미하는 바를 생각해보자.
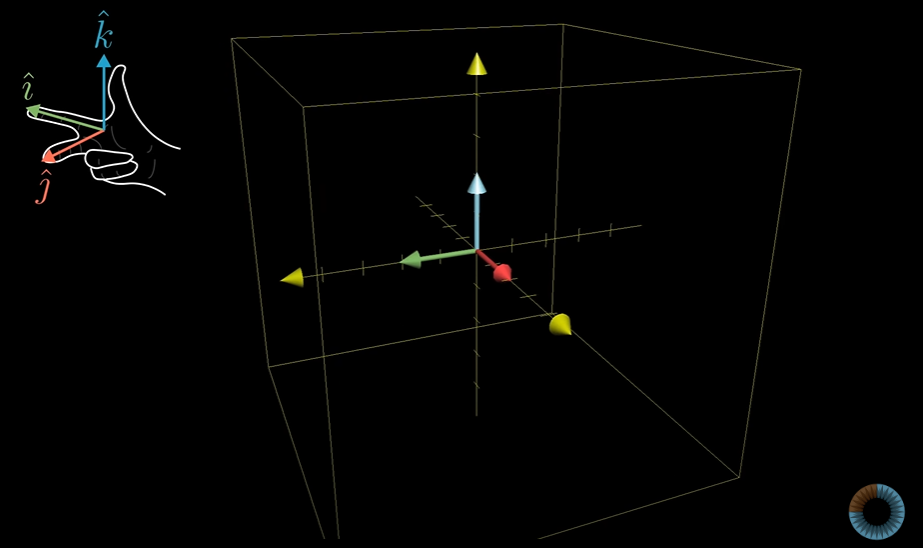
3차원에서의 방향(orientation)에 대해 설명하는 방법으로는 오른손 규칙이 있다
오른손의 집게 손가락이 가르키는 방향이 i-hat방향, 가운데 손가락이 가르키는 방향이 j-hat방향, 엄지 손가락이 가르키는 방향이 k-hat 방향이다.
변환 이후에도 이 방향이 유지되려면, 행렬식 값이 양수여야한다.
변환 이후에 왼손으로 바꿔야 하는 경우에는 방향이 반전된 것이고, 행렬식 값은 음수가 되는 것이다.
[행렬식 공식의 기하학적 증명]
실제로 행렬식을 어떻게 계산하는 지 알기 위해 행렬식의 공식에 대한 증명을 공간의 변환을 통해 알아보자
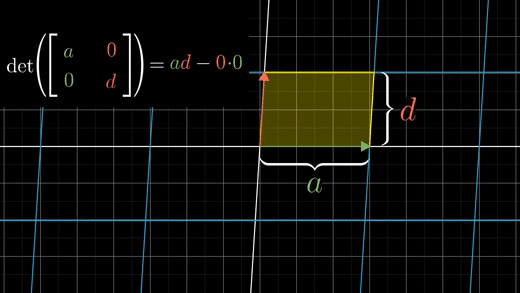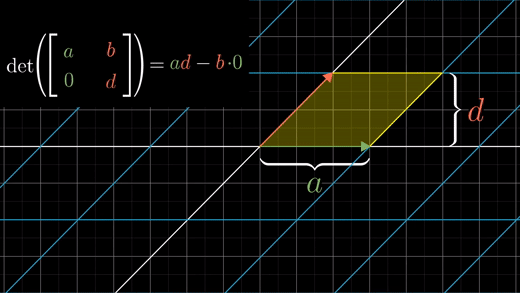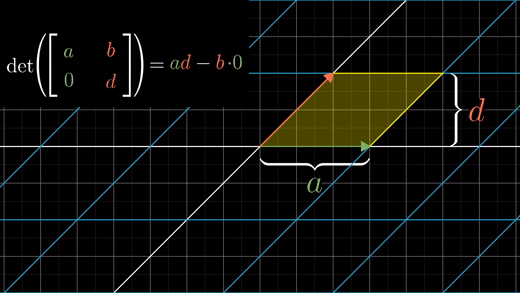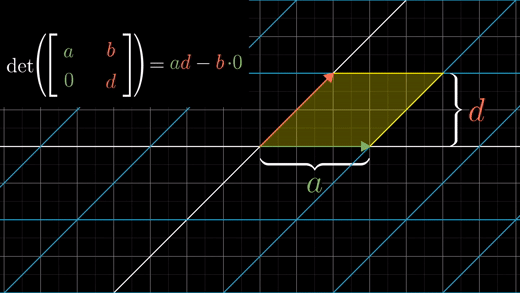
b,c를 둘 다 0이라고 해보자.
a를 i-hat을 x축 방향으로 스케일링하는 요소로 보고,
d의경우에는 j-hat을 y축방향으로 스케일링하는 요소로 보자.
다른값 b,c는 모두 0이기 때문에 행렬식 결과는 a*d가 된다.
그럼 단위 정사각형이 변환 후에 직사각형이 된다.

b.c값 중 하나가 0이라면, 평행사변형을 얻게된다.
밑변 a, 높이 d이기 때문에 a*d로 영역의 크기는 같다.
b,c가 둘 다 0이 아닌 경우라면 b*c값이 알려주는 것은 이 평행사변형의 얼마나 대각선방향으로 눌러지거나 찌그러지는지를 말해준다.
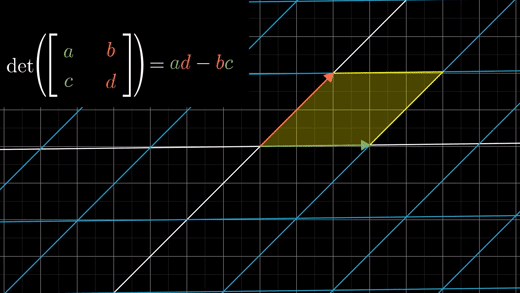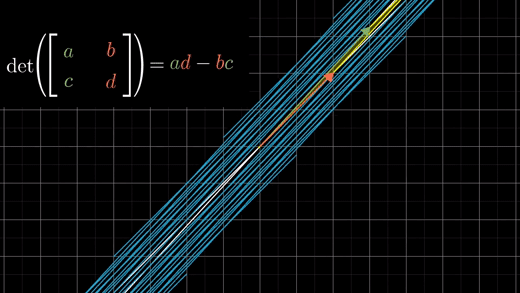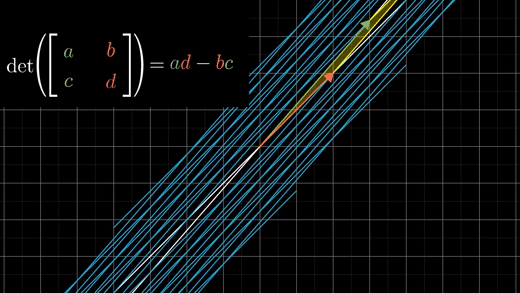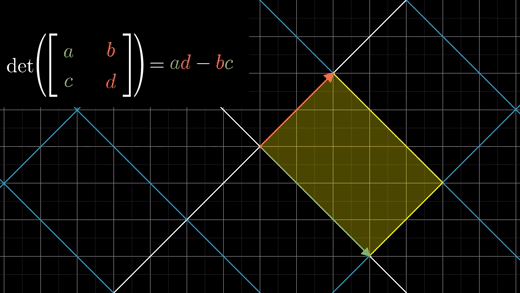
이 모든 것들은 3차원 행렬식 값의 공식에 대해서도 모두 적용가능하다.
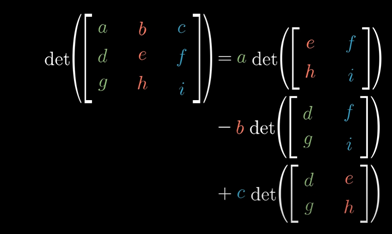
Q) 두 개의 행렬을 곱한 후 얻어지는 행렬식 값은 따로 두 행렬의 행렬식 값을 구해서 곱하는 것과 같을까?
한 문장으로 설명해보기
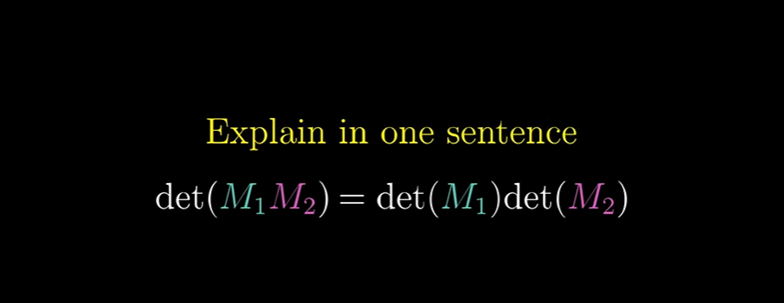
A) 같다. 그 이유는 행렬 두 개를 곱한다는 것은 하나의 변환을 적용한 다음 다른 변환을 적용한다는 것을 의미하기 때문이다.
- 행렬식?
- 공간의 변환 후에 기저 벡터가 이루는 단위 영역이 얼마나 변화되었는지 알려주는 팩터값
'수학 > 선형대수학' 카테고리의 다른 글
{학습 목적}
Chapter 6에서는 행렬식에 대해 학습한다.
행렬식은 앞 챕터에서의 선형 변환, 즉 공간 변형의 개념을 적용하여 이루어지는 것 같다.
앞에서는 공간의 변형을 다뤘다면 이 부분에서는 기저 벡터가 이루는 단위 영역의 개념으로 축소하여 좀 더 깊이 있게 변형을 이해해보는 과정인 것 같다.
즉, 이 개념을 공부하는 이유는 공간의 변형의 개념을 좀 더 축소화한 단위 영역의 변환을 시각적으로 바라보기 위해서라고 생각한다.
<행렬식>
[행렬식]
행렬식(determinant): 선형 변환에 의한 단위 정사각형의 영역의 변화를 나타내는 팩터

예를 들어 행렬식 값이 6이라면, 영역 크기를 6으로 확장하는 것을 의미한다.
2차원 변환의 행렬식 값이 0이라면, 어느 영역이든 크기가 0이기 때문에 모든 공간이 찌그러져서 선이 되거나 점이 될 수 있다.
행렬식 값이 음수값이라면 공간의 방향(orientation)이 뒤집힌다는 의미이다.

이 행렬식의 절대값을 영역 스케일링에 관한 팩터로 볼 수 있다.
[3차원에서의 행렬식]
3차원인 3x3행렬에서의 행렬식 값은 부피가 얼마나 스케일링 되는지를 알려준다.
3차원 행렬에서는 하나의 1x1x1 정육면체에 집중한다.
변환 후 이 정육면체는 기울어진 정육면체가 되는데 이를 평행육면체(parallelepiped)이라고 한다.
즉, 행렬식의 값은 부피 1인 정육면체가 바뀐 후의 평행육면체의 부피를 알려주는 것이다.

+ 앞에서 배웠던 선형 종속의 개념을 생각해보면, 행렬식이 0이라는 것은 공간이 찌그러져서 선이나, 점을 만들기 때문에 벡터들 중 하나가 다른 벡터들의 span에 포함되는 경우이다.
그러므로 그 행렬의 열들이 선형종속(lineary dependent)하다고 할 수 있다.
3차원에서 행렬식의 음수 값이 의미하는 바를 생각해보자.
3차원에서의 방향(orientation)에 대해 설명하는 방법으로는 오른손 규칙이 있다
오른손의 집게 손가락이 가르키는 방향이 i-hat방향, 가운데 손가락이 가르키는 방향이 j-hat방향, 엄지 손가락이 가르키는 방향이 k-hat 방향이다.
변환 이후에도 이 방향이 유지되려면, 행렬식 값이 양수여야한다.
변환 이후에 왼손으로 바꿔야 하는 경우에는 방향이 반전된 것이고, 행렬식 값은 음수가 되는 것이다.

[행렬식 공식의 기하학적 증명]
실제로 행렬식을 어떻게 계산하는 지 알기 위해 행렬식의 공식에 대한 증명을 공간의 변환을 통해 알아보자
b,c를 둘 다 0이라고 해보자.
a를 i-hat을 x축 방향으로 스케일링하는 요소로 보고,
d의경우에는 j-hat을 y축방향으로 스케일링하는 요소로 보자.
다른값 b,c는 모두 0이기 때문에 행렬식 결과는 a*d가 된다.
그럼 단위 정사각형이 변환 후에 직사각형이 된다.

b.c값 중 하나가 0이라면, 평행사변형을 얻게된다.
밑변 a, 높이 d이기 때문에 a*d로 영역의 크기는 같다.

b,c가 둘 다 0이 아닌 경우라면 b*c값이 알려주는 것은 이 평행사변형의 얼마나 대각선방향으로 눌러지거나 찌그러지는지를 말해준다.
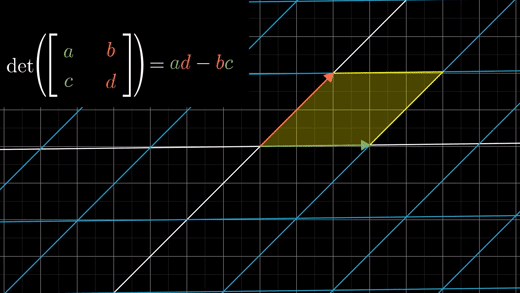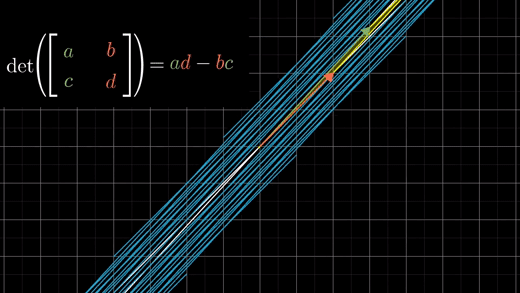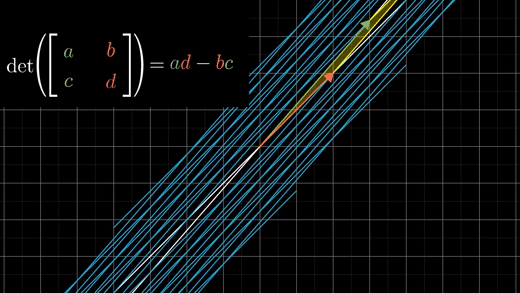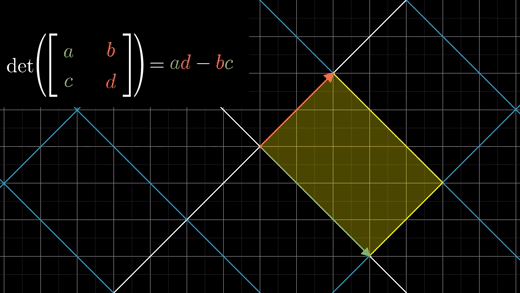
이 모든 것들은 3차원 행렬식 값의 공식에 대해서도 모두 적용가능하다.
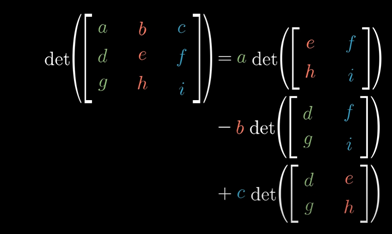
Q) 두 개의 행렬을 곱한 후 얻어지는 행렬식 값은 따로 두 행렬의 행렬식 값을 구해서 곱하는 것과 같을까?
한 문장으로 설명해보기
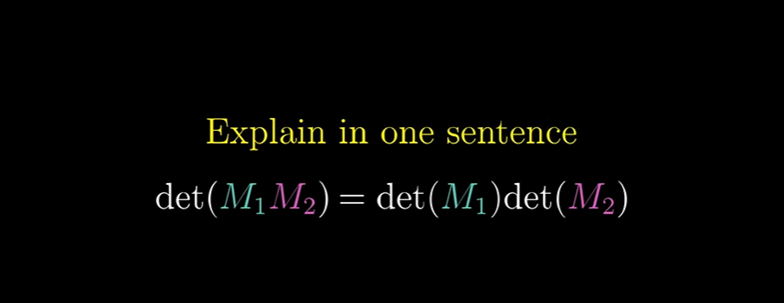
A) 같다. 그 이유는 행렬 두 개를 곱한다는 것은 하나의 변환을 적용한 다음 다른 변환을 적용한다는 것을 의미하기 때문이다.
- 행렬식?
- 공간의 변환 후에 기저 벡터가 이루는 단위 영역이 얼마나 변화되었는지 알려주는 팩터값
