{학습 목적}
Chapter 10에서는 일반적으로 널리 알려져있는 외적의 정의에 대해서 학습한다.
그 다음 챕터에서 배울 외적의 정의를 깊게 이해하기 위한 전 단계이기 때문에 이 파트를 학습하는 것 같다.
이 챕터에서는 이중성에 대한 개념을 다루진 않았는데 내가 예상하기로는 외적과 행렬식 사이에서 이중성이 존재하는 것 같다....
<외적>
외적 파트는 총 2개의 강의 영상으로 구성되어있다.
첫 번째 강의는 일반적인 외적의 개념에 대해 설명한다.
2차원에서의 두 벡터 v,w가 있을 때, 이들이 만드는 평행사변형을 생각해보자.
v 벡터를 복사해서 꼬리를 w 벡터의 끝부분에 맞추고, w 벡터를 복사해서 꼬리를 v벡터의 끝에 맞춘다.
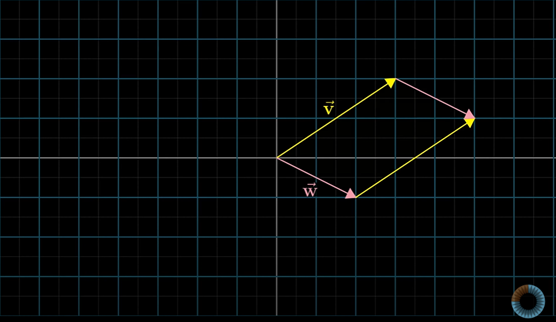
v 벡터와 w 벡터의 외적(cross product)은 ×라는 곱하기 기호를 사용해서 적고, 이 평행사변형의 면적을 의미한다.
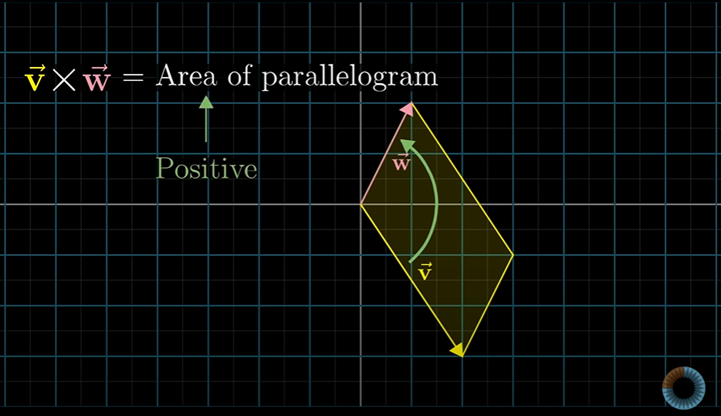
여기에 추가로 방향(orientation)까지 고려해야한다.
기본적으로 v 벡터는 w 벡터의 오른쪽이다. 그래서 v × w의 값은 양수이다.
하지만, v 벡터가 w 벡터의 왼쪽에 존재하는 경우, 외적은 음수가 된다.
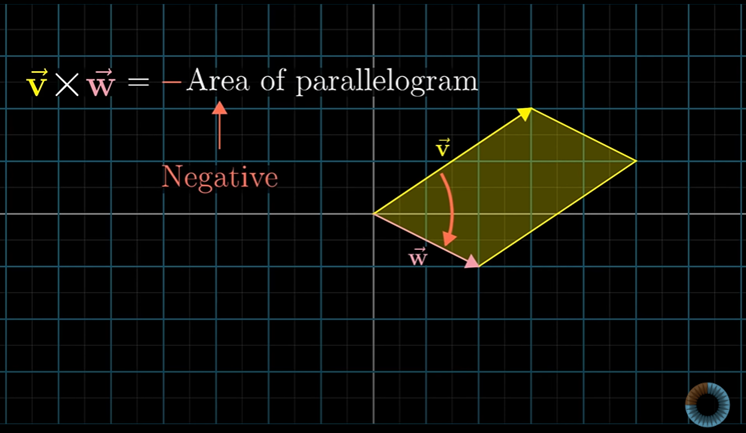
여기서 중요한 것은 순서이다.
순서를 v × w로 기존 w × v와 다르게 바꾸면 외적은 기존 값의 음수가 된다.
순서에 관해 기억하는 방법이있다.
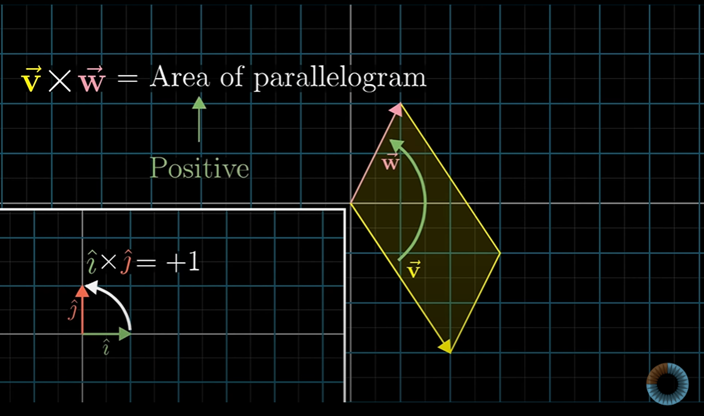
외적 하나를 먼저 구하는 방법인데, 두 기저 벡터를 i × j 순서로 외적을 구해놓는 것이다.
그럼 항상 양수가 나올 것이다.
기저 벡터의 순서는 방향을 정의한 순서이기 때문에 i는 j의 오른쪽이다.
그래서 좀 전에 봤던 v × w에서 양수 값이 나온 이유도 v가 w의 오른쪽이기 때문이라고 볼 수 있다.
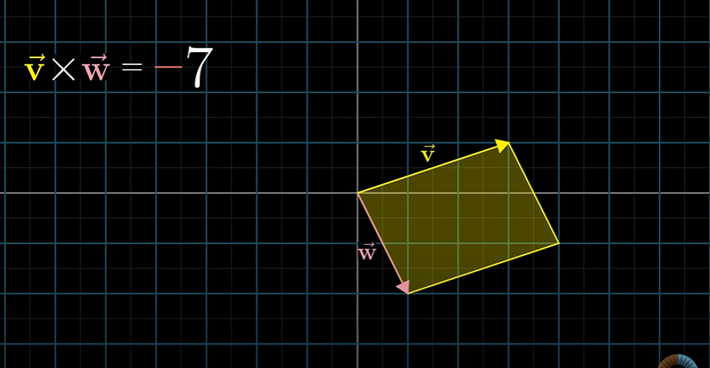
여기 보여준 벡터로 예를 들어, 일단은 면적만을 살펴보면, 평행사변형의 면적은 7이다.
그리고 v가 w의 왼쪽이기 때문에 외적 값은 음수값이 되어야한다.
그러므로 v × w는 -7이다.
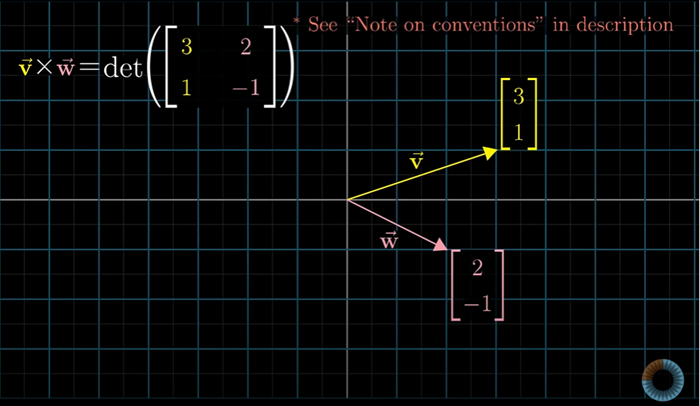
행렬식을 통해 계산으로도 이 면적을 구할 수 있다.
2차원에서 v × w의 외적을 계산하는 방법은 v좌표값을 행렬의 첫번째 열에 적고, w좌표값을 행렬의 두번째 열에 적는다.
그리고 행렬식을 계산하면 된다.
이렇게 하는 이유는 행렬의 열은 각각 v벡터와 w벡터를 나타내고 각각 하나의 선형변환에 대응돼서 기저벡터인 i,j를 v,w로 변환시키기 때문이다.
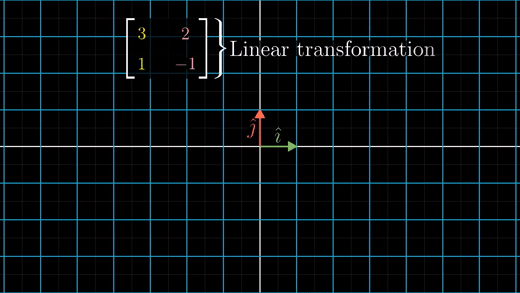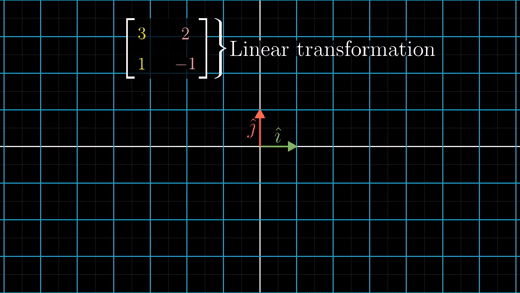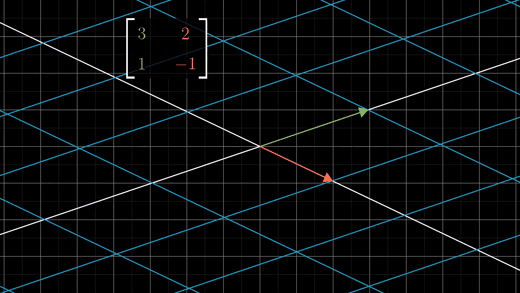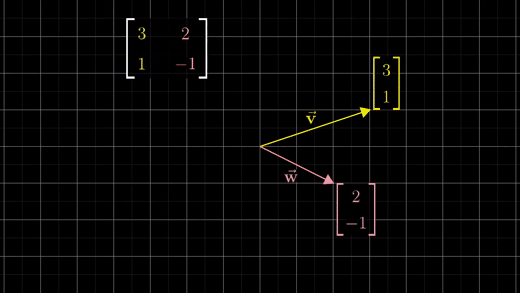
행렬식은 변환에 의해 면적이 얼마나 변하는 지 측정하는 것이다.
변환 전 영역에서는 i,j 기저 벡터가 단위 정사각형을 이루고 있다.
변환 후, 이 정사각형이 변해서 우리가 구하길 원하는 평행사변형이 된다.
그래서 행렬식이라는 소위 면적 변화 요소(factor)을 구하면 이 평행사변형의 면적이 되는 것이다.
평행사변형의 변형 전 출발점이 면적 1인 정사각형이었기 때문이다.
더 나아가서 v벡터가 w벡터의 왼쪽에 있는 경우에는 방향이 변환에 의해 뒤집혔다는 의미니까 결과적으로 행렬식은 음수값이다.
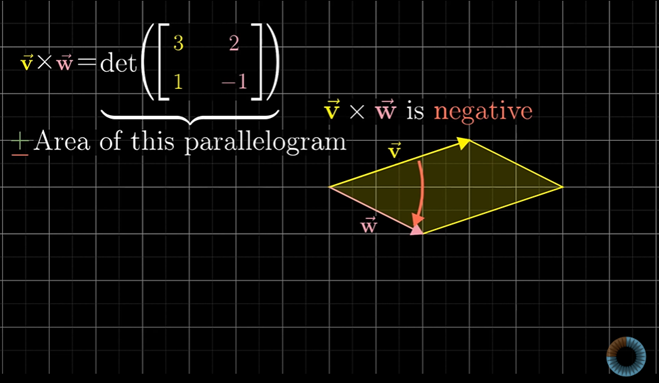
외적을 직관적으로 생각해보자.
두 벡터가 수직이거나 수직에 가까운 상태라면 외적은 두 벡터가 같은 쪽으로 기울어져 있는 경우보다 더 클 것이다.
그 이유는 평행사변형의 면적은 수직에 가까울수록 최대값이 되기 때문이다.
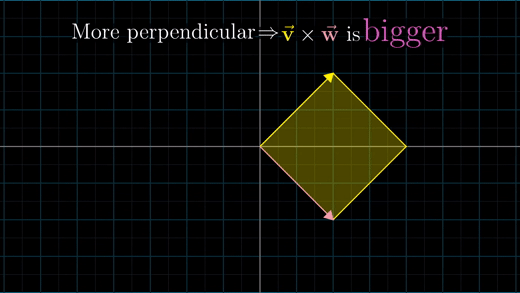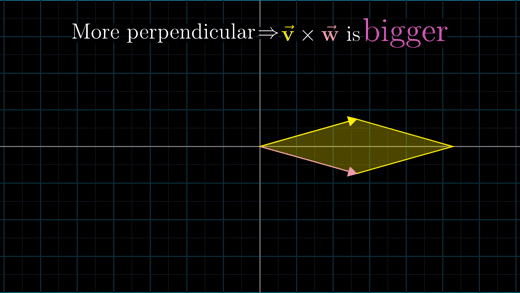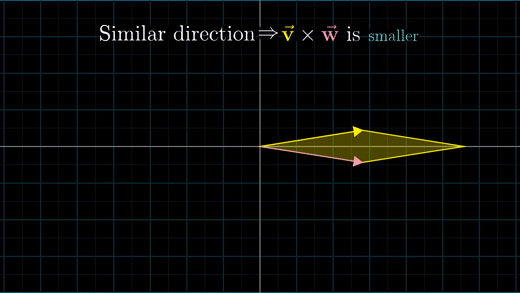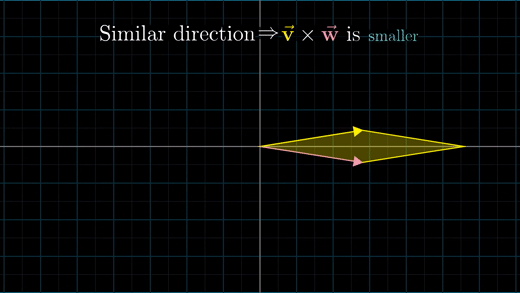
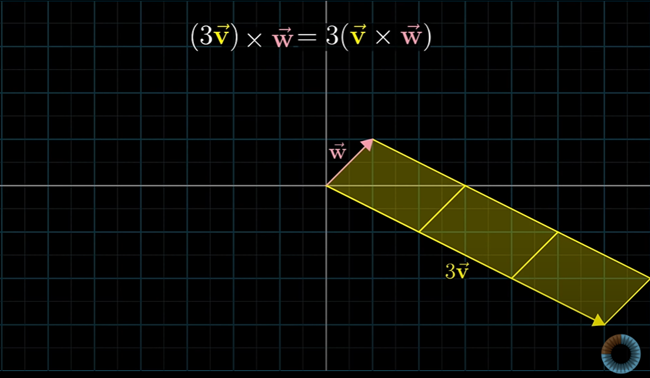
또 다른 하나는, 벡터 하나의 크기를 3으로 늘려보면, 평행사변형의 면적도 3배가 될 것이다.
3v × w 외적값은 정확하게 v × w의 3배가 될 것이다.
하지만 이와 같은 설명은 정확한 외적의 정의는 아니다.
원래 외적이란, 3차원인 두 벡터를 결합해서 새로운 3차원 벡터를 만드는 것이다.
앞에서 했던 것처럼 두 벡터가 만드는 평행사변형을 이용해서 설명한다.
평행사변형 면적이 2.5라고해보자.
말했듯이, 외적 결과는 숫자가 아니라 벡터이다.
이 새 벡터(p)의 길이가 바로 평행사변형의 면적과 같다. 이 경우 그래서 2.5가 된다.
그리고 새 벡터의 방향은 평행사변형에 수직한 방향이다.

하지만 여기서 가능한 p벡터의 2가지 위치에 대해 생각해봐야한다.
이 때, 오른손 규칙을 사용한다.
오른쪽 집게 손가락을 v방향에 놓고, 가운데 손가락을 w방향에 놓는다.
그럼 엄지손가락이 가르키는 방향이 외적의 방향이 된다.
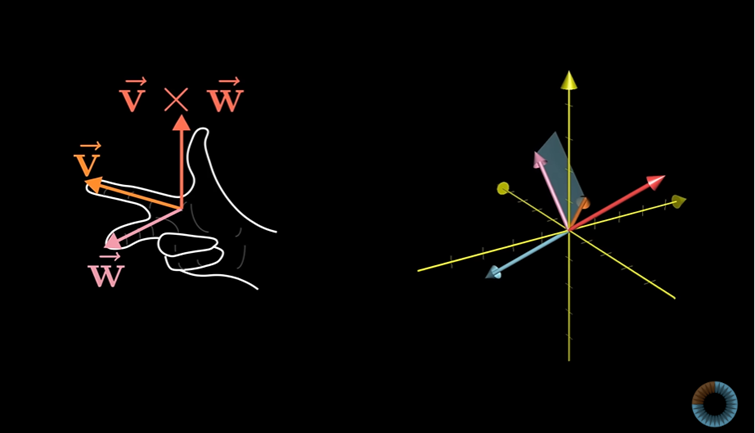
이렇게 외적을 구하는 방법 말고 좀 더 일반적인 경우에 사용할 수 있는 공식이 있다.
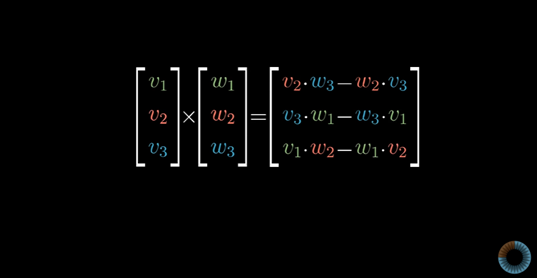
하지만 이 공식을 3차원 행렬식을 포함해서 좀 더 쉽게 이해하는 방법이 있다.
먼저 두번째와 세번째열을 v와 w 벡터로 채우고 첫번째 열은 기저벡터 i,j,k를 적어 3차원 행렬을 만든다.
그리고 나서 행렬식을 계산하면 된다.
여기서 행렬의 요소값으로 벡터를 넣는다는 것은 무슨 의미일까?
이것을 표기적 트릭이라고 일컫는데,
기저벡터 i,j,k 벡터를 하나의 숫자처럼 계산하면, 기저벡터들의 선형조합식을 얻게된다.
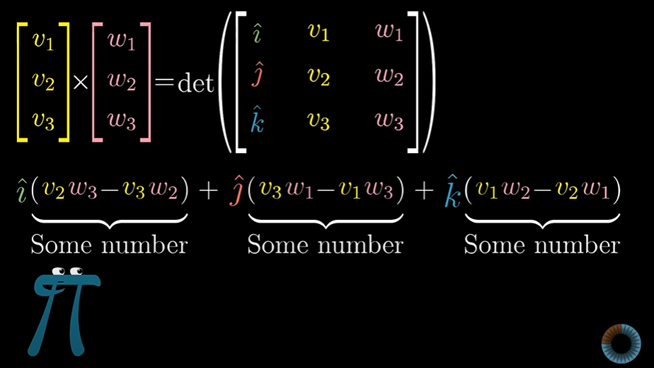
이 결과로 나온 벡터는 해당하는 평행사변형 면적과 같으면서 방향은 오른손 법칙을 따르는 유일한 벡터이다.
- 외적?
- 기저 벡터가 변환 후 만드는 평행사변형의 면적(크기)에 오른손 규칙을 고려한 방향이 있는 벡터
'수학 > 선형대수학' 카테고리의 다른 글
{학습 목적}
Chapter 10에서는 일반적으로 널리 알려져있는 외적의 정의에 대해서 학습한다.
그 다음 챕터에서 배울 외적의 정의를 깊게 이해하기 위한 전 단계이기 때문에 이 파트를 학습하는 것 같다.
이 챕터에서는 이중성에 대한 개념을 다루진 않았는데 내가 예상하기로는 외적과 행렬식 사이에서 이중성이 존재하는 것 같다....
<외적>
외적 파트는 총 2개의 강의 영상으로 구성되어있다.
첫 번째 강의는 일반적인 외적의 개념에 대해 설명한다.
2차원에서의 두 벡터 v,w가 있을 때, 이들이 만드는 평행사변형을 생각해보자.
v 벡터를 복사해서 꼬리를 w 벡터의 끝부분에 맞추고, w 벡터를 복사해서 꼬리를 v벡터의 끝에 맞춘다.

v 벡터와 w 벡터의 외적(cross product)은 ×라는 곱하기 기호를 사용해서 적고, 이 평행사변형의 면적을 의미한다.
여기에 추가로 방향(orientation)까지 고려해야한다.
기본적으로 v 벡터는 w 벡터의 오른쪽이다. 그래서 v × w의 값은 양수이다.

하지만, v 벡터가 w 벡터의 왼쪽에 존재하는 경우, 외적은 음수가 된다.

여기서 중요한 것은 순서이다.
순서를 v × w로 기존 w × v와 다르게 바꾸면 외적은 기존 값의 음수가 된다.
순서에 관해 기억하는 방법이있다.
외적 하나를 먼저 구하는 방법인데, 두 기저 벡터를 i × j 순서로 외적을 구해놓는 것이다.
그럼 항상 양수가 나올 것이다.
기저 벡터의 순서는 방향을 정의한 순서이기 때문에 i는 j의 오른쪽이다.
그래서 좀 전에 봤던 v × w에서 양수 값이 나온 이유도 v가 w의 오른쪽이기 때문이라고 볼 수 있다.

여기 보여준 벡터로 예를 들어, 일단은 면적만을 살펴보면, 평행사변형의 면적은 7이다.
그리고 v가 w의 왼쪽이기 때문에 외적 값은 음수값이 되어야한다.
그러므로 v × w는 -7이다.

행렬식을 통해 계산으로도 이 면적을 구할 수 있다.
2차원에서 v × w의 외적을 계산하는 방법은 v좌표값을 행렬의 첫번째 열에 적고, w좌표값을 행렬의 두번째 열에 적는다.
그리고 행렬식을 계산하면 된다.

이렇게 하는 이유는 행렬의 열은 각각 v벡터와 w벡터를 나타내고 각각 하나의 선형변환에 대응돼서 기저벡터인 i,j를 v,w로 변환시키기 때문이다.

행렬식은 변환에 의해 면적이 얼마나 변하는 지 측정하는 것이다.
변환 전 영역에서는 i,j 기저 벡터가 단위 정사각형을 이루고 있다.
변환 후, 이 정사각형이 변해서 우리가 구하길 원하는 평행사변형이 된다.
그래서 행렬식이라는 소위 면적 변화 요소(factor)을 구하면 이 평행사변형의 면적이 되는 것이다.
평행사변형의 변형 전 출발점이 면적 1인 정사각형이었기 때문이다.
더 나아가서 v벡터가 w벡터의 왼쪽에 있는 경우에는 방향이 변환에 의해 뒤집혔다는 의미니까 결과적으로 행렬식은 음수값이다.
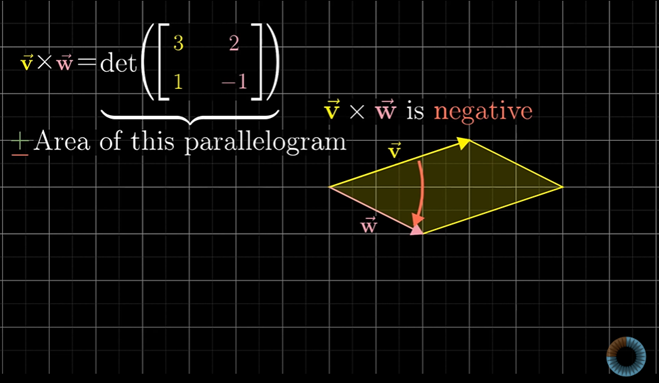
외적을 직관적으로 생각해보자.
두 벡터가 수직이거나 수직에 가까운 상태라면 외적은 두 벡터가 같은 쪽으로 기울어져 있는 경우보다 더 클 것이다.
그 이유는 평행사변형의 면적은 수직에 가까울수록 최대값이 되기 때문이다.

또 다른 하나는, 벡터 하나의 크기를 3으로 늘려보면, 평행사변형의 면적도 3배가 될 것이다.
3v × w 외적값은 정확하게 v × w의 3배가 될 것이다.

하지만 이와 같은 설명은 정확한 외적의 정의는 아니다.
원래 외적이란, 3차원인 두 벡터를 결합해서 새로운 3차원 벡터를 만드는 것이다.
앞에서 했던 것처럼 두 벡터가 만드는 평행사변형을 이용해서 설명한다.
평행사변형 면적이 2.5라고해보자.
말했듯이, 외적 결과는 숫자가 아니라 벡터이다.
이 새 벡터(p)의 길이가 바로 평행사변형의 면적과 같다. 이 경우 그래서 2.5가 된다.
그리고 새 벡터의 방향은 평행사변형에 수직한 방향이다.

하지만 여기서 가능한 p벡터의 2가지 위치에 대해 생각해봐야한다.
이 때, 오른손 규칙을 사용한다.
오른쪽 집게 손가락을 v방향에 놓고, 가운데 손가락을 w방향에 놓는다.
그럼 엄지손가락이 가르키는 방향이 외적의 방향이 된다.
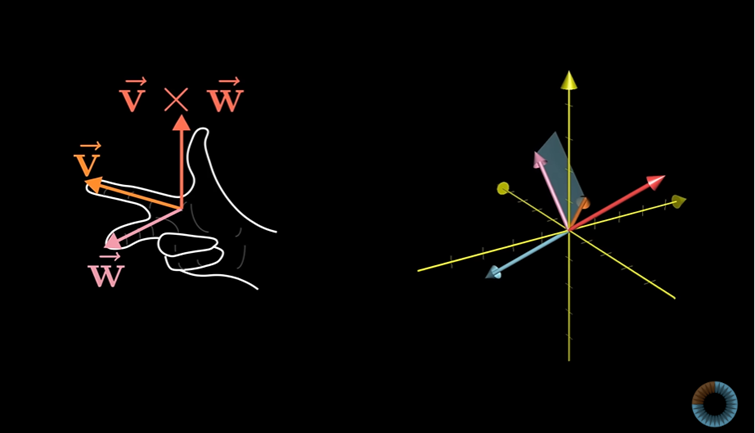
이렇게 외적을 구하는 방법 말고 좀 더 일반적인 경우에 사용할 수 있는 공식이 있다.
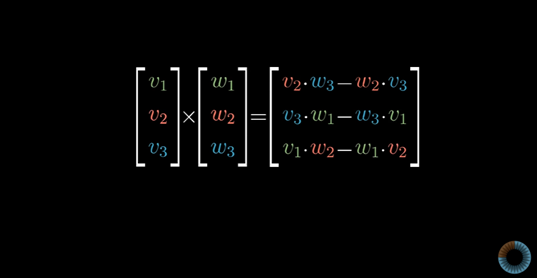
하지만 이 공식을 3차원 행렬식을 포함해서 좀 더 쉽게 이해하는 방법이 있다.
먼저 두번째와 세번째열을 v와 w 벡터로 채우고 첫번째 열은 기저벡터 i,j,k를 적어 3차원 행렬을 만든다.
그리고 나서 행렬식을 계산하면 된다.
여기서 행렬의 요소값으로 벡터를 넣는다는 것은 무슨 의미일까?
이것을 표기적 트릭이라고 일컫는데,
기저벡터 i,j,k 벡터를 하나의 숫자처럼 계산하면, 기저벡터들의 선형조합식을 얻게된다.
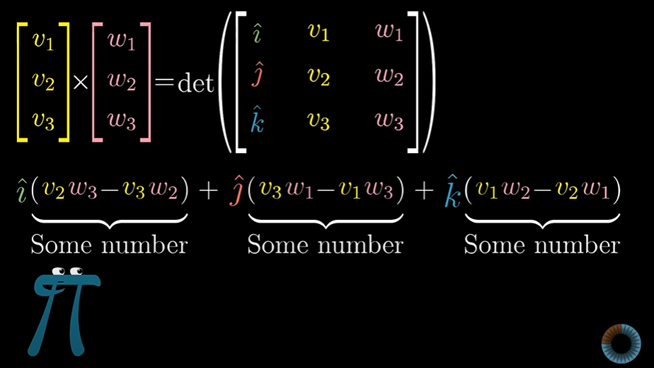
이 결과로 나온 벡터는 해당하는 평행사변형 면적과 같으면서 방향은 오른손 법칙을 따르는 유일한 벡터이다.
- 외적?
- 기저 벡터가 변환 후 만드는 평행사변형의 면적(크기)에 오른손 규칙을 고려한 방향이 있는 벡터
