{학습 목적}
Chapter 16에서는 함수의 예시를 들어 수학에서 벡터와 비슷한 개념들이 많다는 것을 알려주고 있다.
이 부분을 학습하는 이유는 벡터가 우리가 생각하는 좌표계에서의 화살표와 같이 특정한 것이 아니라 공리만 만족하게 된다면 여러 공간에서 쓰일 수 있다는 것을 배우기 위해서라고 생각한다.
즉, 벡터와 행렬이 광범위하게 쓰인다는 것을 깨달을 수 있었다.
<추상적인 벡터 공간>
이 선형대수 강의에서 가장 처음으로 했던 질문은
"벡터란 무엇일까?" 이었다.
2차원 벡터란 근본은 평면에 있는 화살표인데 편의상 좌표계를 그린 것인가, 아니면 원래는 실수쌍인데 보기 쉽게 평면에 화살표로 표현한 것인가?
또는 둘 다 더 근본적인 무엇을 나타내는 도구일 뿐인가?
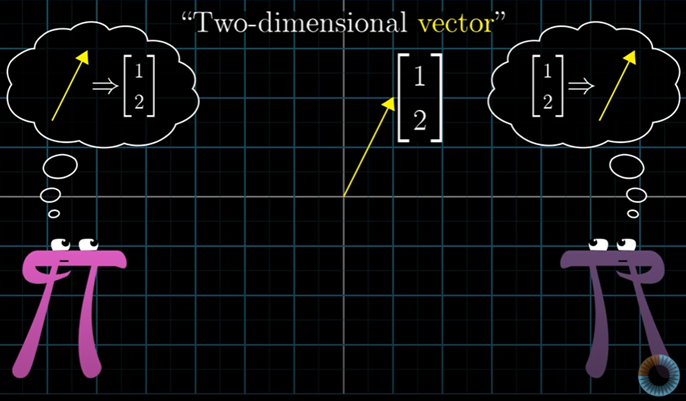
벡터를 숫자의 배열로 정의하면 명백한 것 같다.
즉 4차원 벡터나 100차원 벡터도 실제로 존재해서 다룰 수 있는 개념처럼 보인다.
다른 한편으로 4차원은 막연해서 기하학적으로는 설명하기 어렵다.
반면 선형대수에서는특히 기저벡터를 바꾸는데 능숙할수록 주어진 좌표계와 상관없이 공간을 다룬다.
게다가 좌표계는 기저벡터를 어떻게 정하냐에 따라 수시로 바뀐다.
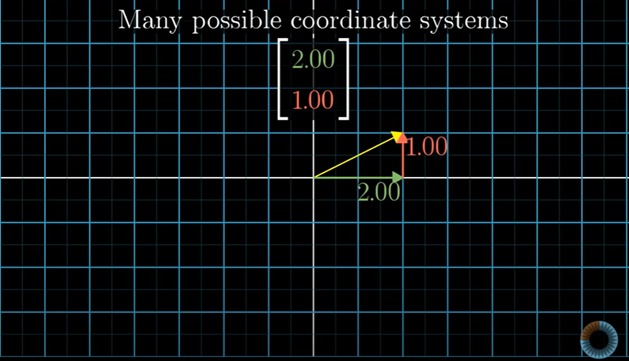
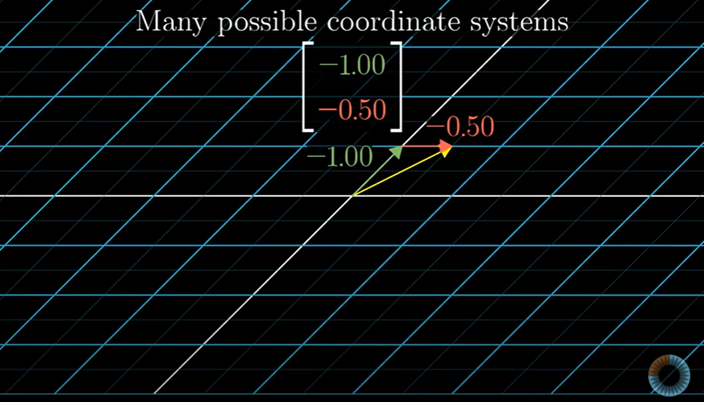
determinant나 고유벡터처럼 선형대수에서 중요한 주제는 좌표계를 어떻게 정하는지랑 상관이 없다.
determinant는 변환이 면적을 얼마나 스케일링하는지를 나타내며
고유벡터는 변환이 일어나도 span을 벗어나지 않는 벡터이다.

하지만 이 둘은 공간의 성질이며 하나를 원래 값으로 일정하게 유지한 채로 좌표계를 자유롭게 바꿀 수 있다.
만약 벡터가 실수의 배열이 아니고 공간적인 본질을 가지고 있는 것이라면 '공간'이란 무엇일까?
‘공간’이 무엇인지 자세히 설명하기 위해 화살표나 수의 배열이 아니라 벡터 같은 값, 즉 ‘함수’에 대해 이 챕터에서 학습한다.
함수는 그냥 다른 종류의 벡터일 뿐이라는 말이다.
두 벡터를 더하는 것과 같은 방법으로, 두 함수 f와g를 더해서 새로운 함수 f+g를 구하는 합리적인 방법이 있다.
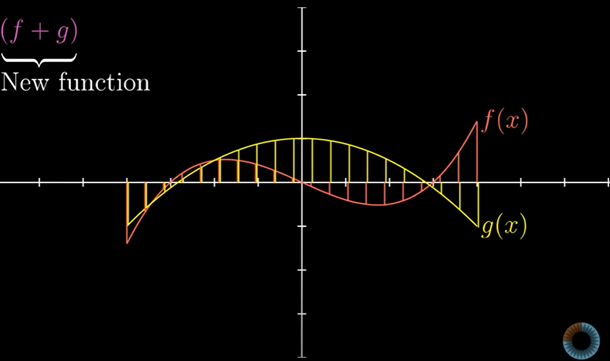
-4처럼 어떤 값이 주어지면 새로운 함수의 함수 값은 동일하게 주어진 값 -4에서 계산한 f와 g의 함수값의 합이다.
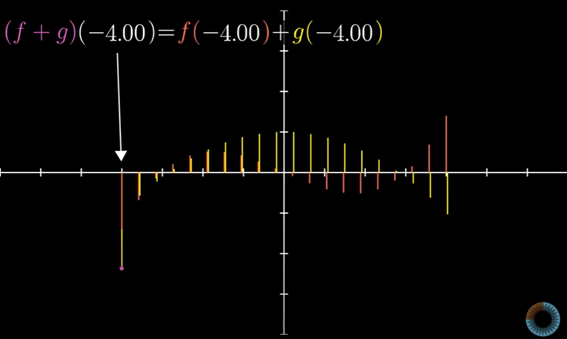
더 일반적으로, 임의의 값 x에서 f+g의 함수값은 f(x)와 g(x)의 합이다.
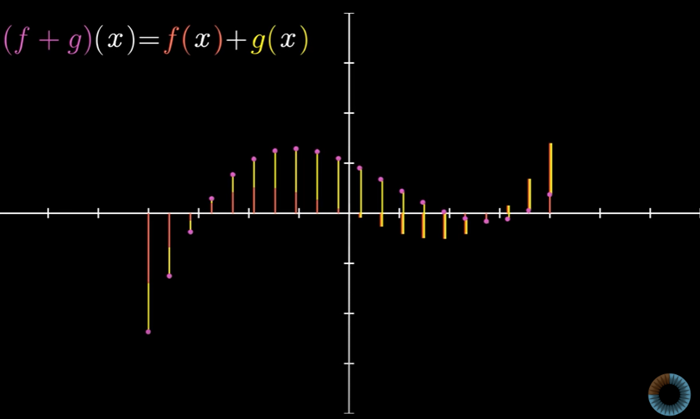
이건 벡터에서 같은 좌표계끼리 더하는 것과 비슷한데 함수에서는 무한히 많은 좌표계들을 더하는 셈이다.
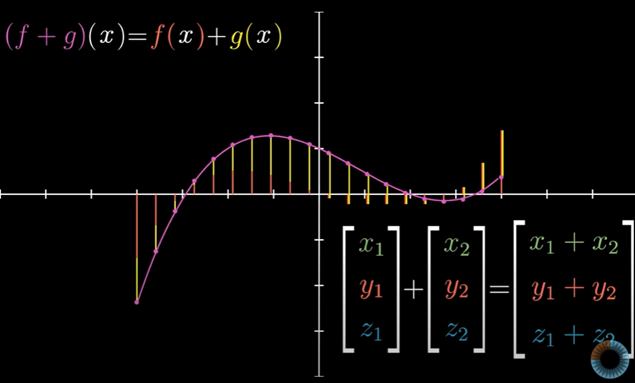
비슷하게 함수를 실수배하는 합리적인 방법도 있다.
그냥 모든 함수값에 실수를 곱하는 것이다.
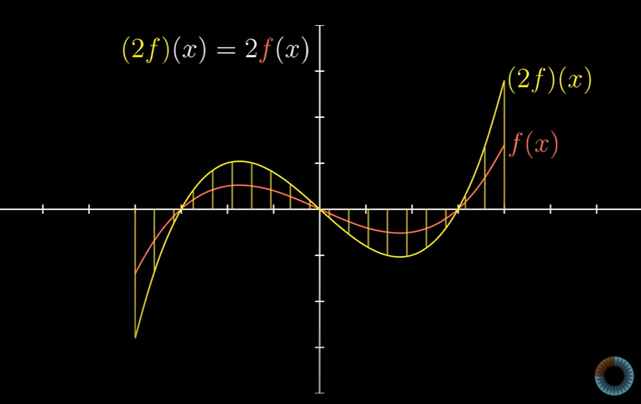
마찬가지로 벡터에서 좌표계마다 실수배 하는 것과 비슷한데
무한히 많은 좌표계에 실수배를 하는 셈이다.
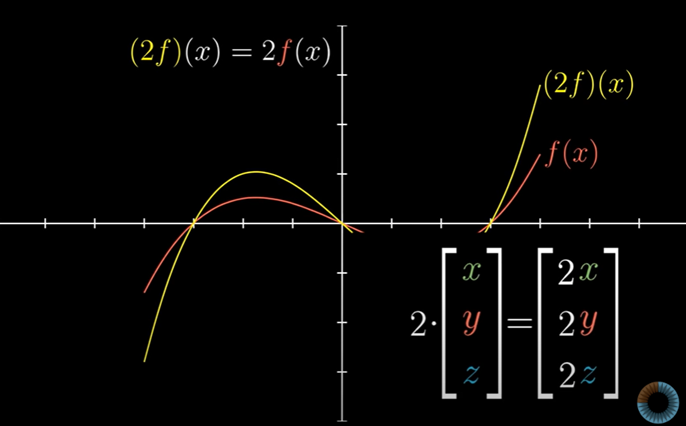
벡터를 가지고 더하거나 실수배만 한다고 하면, 공간상의 화살표로부터 처음에 생각했던 선형대수의 구조와 문제풀이 방법을 함수에도 똑같이 적용할 수 있다.
예를 들면, 한 함수를 매우 합리적으로 다른 함수로 바꿔주는 함수에 대한 선형변환이 있다.
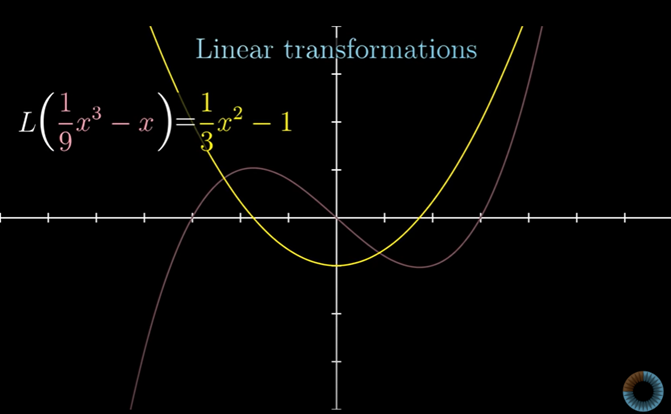
미적분학에서 나오는 친숙한 예시가 바로 도함수이다.
이건 한 함수를 다른 함수로 바꾸는 변환이다.
함수에서는가끔씩 변환 대신 연산이라고 부르는 것을 볼 수 있는데 의미는 똑같다.
선형성에 대한 수학적 정의는 일반적이라서 벡터만이 아니라 함수에도 적용할 수 있다.
변환이 선형이라면 합과 실수배 성질을 만족한다.
합의 성질이란 두 벡터 v,w를 더하고 그 결과를 반환한 것과 v와 w를 먼저 변환하고 더한 것과 같다는 것이다.


실수배 성질이란 벡터 v를 실수배 하고 변환한 것과 v를 먼저 변환하고 실수배한 것이 같다는 것이다.

이런 것을 “선형변환이 합과 실수배를 보존한다”고 한다.
변환 후에도 격자가 평행하고 균등하게 유지되는 건 2차원 평면 위의 점들이 바로 이 두 성질을 만족하기 때문이다.
또 이 성질은 행렬과 벡터의 곱을 가능하게 만들어서 기저벡터에 따라 선형변환을 완벽히 표현할 수 있게 한다.
어떤 벡터든지 기저벡터의 실수배와 합으로 표현할 수 있기 때문에 벡터를 변환한 결과 역시 기저벡터를 변환한 것의 실수배의 합으로 표현할 수 있다.
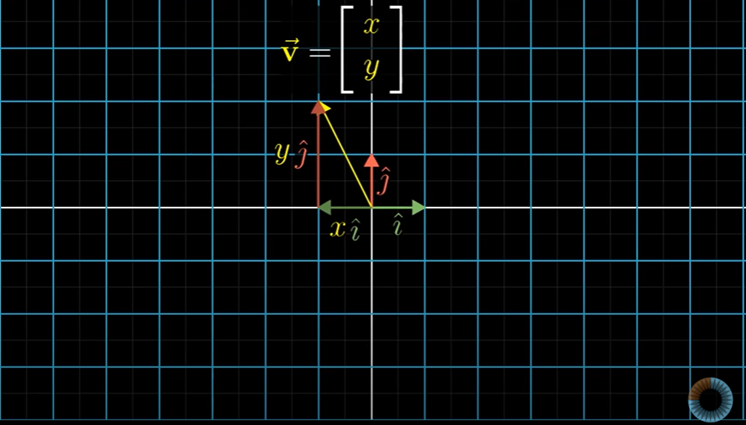
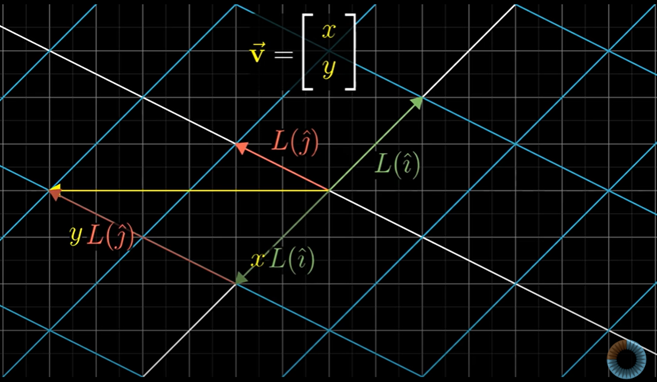
함수에서도 이 방법이 성립된다.
예를 들어 미적분학에서는 미분할 때 합과 실수배 성질을 자연스럽게 사용한다.
두 함수를 더한 후, 미분한 것은 각각을 먼저 미분하고 그 다음 더한 것과 같다.

마찬가지로 함수를 실수배한 후, 미분한 것은 먼저 미분하고 실수배 한 것과 같다.

행렬과 함수가 비슷한지 보기 위해 미분을 행렬과 같이 기술해보자
여기서는 함수를 무한차원으로 봐야한다.
각각의 다항식들은 무한히 많은 항을 가질 순 없지만, 임의의 최고차항을 가질 수 있다.
(여기서 함수가 임의의 최고차항을 갖는다는 의미는 함수의 항들을 확장하게 되면 기저벡터도 무한해지기 때문에
벡터와 행렬의 유사성을 설명하기 위한 표현이다.)

먼저, 기저를 정해 이 공간에서 쓸 좌표계를 정해야한다.
다항식은 이미 변수x 의 거듭제곱 합으로 써 있어서 x의 거듭제곱들로 기저함수를 정하는 것은 자연스럽다.
다시 말해 첫번째 기저함수는 상수함수 1이고, 두번째 기저함수는 x, 그리고 x^2, x^3의 순서가 된다.

이 기저함수의 역할은 벡터에서 i-hat, j-hat, k-hat과 같다.
다항식이 임의의 최고차항을 가지기 때문에 기저함수는 무한히 많다.
그러므로 x^2+3x+5는 5,3,1과 무한히 많은 0을 좌표로 갖는다.
우리는 이것을 첫 기저함수에 5를 곱하고 두번째 기저함수에 3을 곱하고 세번째 기저함수에 1을 곱하고
다른 기저함수는 더하지 않는 것으로 보면 된다.

4x^7- 5x^2의 좌표값은 0,0,-5,0,0,0,4 그 뒤론 무한하게 0이다.

일반적으로, 각 다항식은 유한히 많은 항을 가지고 있어서 그 좌표 역시 유한한 수의 수와 무한히 많은 0으로 이루어진다.

이런 좌표 시스템에서 미분은 대부분 0이고 옆 대각선은 양수인 무한 행렬로 표현할 수 있다.
직접 이 행렬을 구해보자

x^3+5x^2+4x+5를 나타내는 좌표를 행렬 오른쪽에 쓴다.
첫번째 좌표에 영향을 주는 항은 1x4밖에 없다.
즉 상수항은 4가 된다.

이는 4x를 미분해서 4가 나온것과 일치한다.
행렬과 벡터의 곱에서 두 번째 좌표는 2x5이다. 이는 미분결과 x의 계수가 10이라는 것을 말한다.

역시 5x^2를 미분한 결과와 일치한다.
마찬가지로 행렬과 벡터의 곱에서 세 번째 항은 3x1이다.
x^3을 미분하면 3x^2가 되는 것과 일치한다.

나머지는 다 0이다.
이것이 가능한 이유는 미분이 선형이기 때문이다.
각 기저함수를 미분한 뒤 각 열에 집어넣으면 행렬을 구할 수 있다

행렬-벡터 곱과 미분은 겉보기엔 완전히 달라보였지만 알고보면 같은 종류이다.
정리하자면,
선형대수에서의 벡터를 화살표로 보고 내적, 고유벡터 같은 대부분의 개념은 함수에서도 사용되는 개념이다.
대신 내적 또는 고유함수처럼 다른 단어를 쓴다.
즉, 수학에서 벡터와 비슷하게 쓰이는 개념들은 매우 많다.
화살표, 숫자 배열, 함수 같이 벡터와 비슷한 것들의 집합을 벡터 공간이라고 한다.
우리는 벡터 공간의 모든 종류에 대해 다루고 싶지 않기 때문에 벡터 합과 실수배에서 파생된 규칙을 정립해야 한다. 이를 공리(Axioms)라고 부른다.

이 공리들은 내가 생각하는 벡터공간과 새로운 벡터공간에 그 이론을 적용하고 싶은 사람을 연결해주는 다리이다.
그래서 다른 사람의 공간에서의 벡터 정의가 이 공리를 만족한다면 다른건 고려하지 않고도 선형대수의 결론을 적용할 수 있다.
다시 말해, 결론을 구체적인 종류의 벡터로 표현하는 것이 아니라 공리들의 관점에서만 보는 것이다.
그래서 Chapter1 에서 수학자들은 벡터를 "합과 실수배가 공리를 만족하게 정의되어 있으면 무엇이든 벡터가 될 수 있다."고 보는 것이다.
즉, 선형대수학은 벡터를 화살표로 보는 것보다 더 광범위하게 적용할 수 있는 것이다.
- 공리?
- 새로운 벡터 공간에서 벡터와 비슷한 것들의 정의를 검증해볼 때 사용하는 일종의 체크리스트
'수학 > 선형대수학' 카테고리의 다른 글
| [3Blue1Brown] Chapter 12 | 크래머 공식의 기하학적 설명 (0) | 2022.08.08 |
|---|---|
| [3Blue1Brown] Chapter 15 | A quick trick for computing eigenvalues (0) | 2022.08.07 |
| [3Blue1Brown] Chapter 14 | Eigenvectors and eigenvalues (0) | 2022.08.07 |
| [3Blue1Brown] Chapter 13 | Change of basis (0) | 2022.08.06 |
| [3Blue1Brown] Chapter 11 | Cross products in the light of linear transformations (0) | 2022.08.04 |
{학습 목적}
Chapter 16에서는 함수의 예시를 들어 수학에서 벡터와 비슷한 개념들이 많다는 것을 알려주고 있다.
이 부분을 학습하는 이유는 벡터가 우리가 생각하는 좌표계에서의 화살표와 같이 특정한 것이 아니라 공리만 만족하게 된다면 여러 공간에서 쓰일 수 있다는 것을 배우기 위해서라고 생각한다.
즉, 벡터와 행렬이 광범위하게 쓰인다는 것을 깨달을 수 있었다.
<추상적인 벡터 공간>
이 선형대수 강의에서 가장 처음으로 했던 질문은
"벡터란 무엇일까?" 이었다.
2차원 벡터란 근본은 평면에 있는 화살표인데 편의상 좌표계를 그린 것인가, 아니면 원래는 실수쌍인데 보기 쉽게 평면에 화살표로 표현한 것인가?
또는 둘 다 더 근본적인 무엇을 나타내는 도구일 뿐인가?

벡터를 숫자의 배열로 정의하면 명백한 것 같다.
즉 4차원 벡터나 100차원 벡터도 실제로 존재해서 다룰 수 있는 개념처럼 보인다.
다른 한편으로 4차원은 막연해서 기하학적으로는 설명하기 어렵다.
반면 선형대수에서는특히 기저벡터를 바꾸는데 능숙할수록 주어진 좌표계와 상관없이 공간을 다룬다.
게다가 좌표계는 기저벡터를 어떻게 정하냐에 따라 수시로 바뀐다.


determinant나 고유벡터처럼 선형대수에서 중요한 주제는 좌표계를 어떻게 정하는지랑 상관이 없다.
determinant는 변환이 면적을 얼마나 스케일링하는지를 나타내며
고유벡터는 변환이 일어나도 span을 벗어나지 않는 벡터이다.

하지만 이 둘은 공간의 성질이며 하나를 원래 값으로 일정하게 유지한 채로 좌표계를 자유롭게 바꿀 수 있다.
만약 벡터가 실수의 배열이 아니고 공간적인 본질을 가지고 있는 것이라면 '공간'이란 무엇일까?
‘공간’이 무엇인지 자세히 설명하기 위해 화살표나 수의 배열이 아니라 벡터 같은 값, 즉 ‘함수’에 대해 이 챕터에서 학습한다.
함수는 그냥 다른 종류의 벡터일 뿐이라는 말이다.
두 벡터를 더하는 것과 같은 방법으로, 두 함수 f와g를 더해서 새로운 함수 f+g를 구하는 합리적인 방법이 있다.

-4처럼 어떤 값이 주어지면 새로운 함수의 함수 값은 동일하게 주어진 값 -4에서 계산한 f와 g의 함수값의 합이다.

더 일반적으로, 임의의 값 x에서 f+g의 함수값은 f(x)와 g(x)의 합이다.
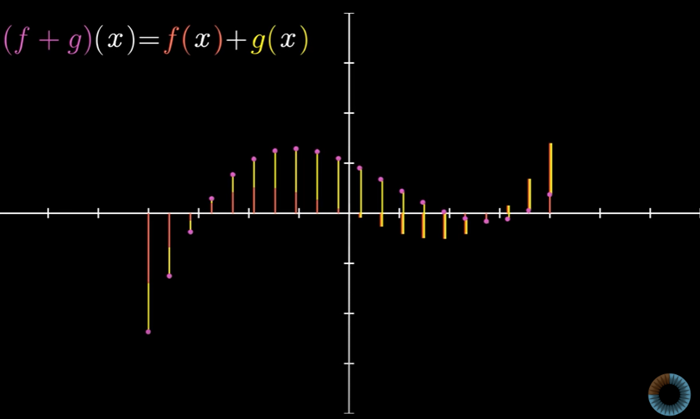
이건 벡터에서 같은 좌표계끼리 더하는 것과 비슷한데 함수에서는 무한히 많은 좌표계들을 더하는 셈이다.

비슷하게 함수를 실수배하는 합리적인 방법도 있다.
그냥 모든 함수값에 실수를 곱하는 것이다.

마찬가지로 벡터에서 좌표계마다 실수배 하는 것과 비슷한데
무한히 많은 좌표계에 실수배를 하는 셈이다.
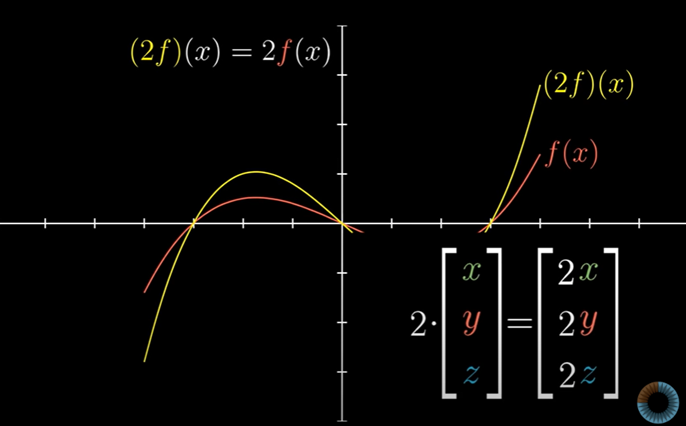
벡터를 가지고 더하거나 실수배만 한다고 하면, 공간상의 화살표로부터 처음에 생각했던 선형대수의 구조와 문제풀이 방법을 함수에도 똑같이 적용할 수 있다.
예를 들면, 한 함수를 매우 합리적으로 다른 함수로 바꿔주는 함수에 대한 선형변환이 있다.

미적분학에서 나오는 친숙한 예시가 바로 도함수이다.
이건 한 함수를 다른 함수로 바꾸는 변환이다.
함수에서는가끔씩 변환 대신 연산이라고 부르는 것을 볼 수 있는데 의미는 똑같다.
선형성에 대한 수학적 정의는 일반적이라서 벡터만이 아니라 함수에도 적용할 수 있다.
변환이 선형이라면 합과 실수배 성질을 만족한다.
합의 성질이란 두 벡터 v,w를 더하고 그 결과를 반환한 것과 v와 w를 먼저 변환하고 더한 것과 같다는 것이다.


실수배 성질이란 벡터 v를 실수배 하고 변환한 것과 v를 먼저 변환하고 실수배한 것이 같다는 것이다.

이런 것을 “선형변환이 합과 실수배를 보존한다”고 한다.
변환 후에도 격자가 평행하고 균등하게 유지되는 건 2차원 평면 위의 점들이 바로 이 두 성질을 만족하기 때문이다.
또 이 성질은 행렬과 벡터의 곱을 가능하게 만들어서 기저벡터에 따라 선형변환을 완벽히 표현할 수 있게 한다.
어떤 벡터든지 기저벡터의 실수배와 합으로 표현할 수 있기 때문에 벡터를 변환한 결과 역시 기저벡터를 변환한 것의 실수배의 합으로 표현할 수 있다.


함수에서도 이 방법이 성립된다.
예를 들어 미적분학에서는 미분할 때 합과 실수배 성질을 자연스럽게 사용한다.
두 함수를 더한 후, 미분한 것은 각각을 먼저 미분하고 그 다음 더한 것과 같다.

마찬가지로 함수를 실수배한 후, 미분한 것은 먼저 미분하고 실수배 한 것과 같다.

행렬과 함수가 비슷한지 보기 위해 미분을 행렬과 같이 기술해보자
여기서는 함수를 무한차원으로 봐야한다.
각각의 다항식들은 무한히 많은 항을 가질 순 없지만, 임의의 최고차항을 가질 수 있다.
(여기서 함수가 임의의 최고차항을 갖는다는 의미는 함수의 항들을 확장하게 되면 기저벡터도 무한해지기 때문에
벡터와 행렬의 유사성을 설명하기 위한 표현이다.)

먼저, 기저를 정해 이 공간에서 쓸 좌표계를 정해야한다.
다항식은 이미 변수x 의 거듭제곱 합으로 써 있어서 x의 거듭제곱들로 기저함수를 정하는 것은 자연스럽다.
다시 말해 첫번째 기저함수는 상수함수 1이고, 두번째 기저함수는 x, 그리고 x^2, x^3의 순서가 된다.

이 기저함수의 역할은 벡터에서 i-hat, j-hat, k-hat과 같다.
다항식이 임의의 최고차항을 가지기 때문에 기저함수는 무한히 많다.
그러므로 x^2+3x+5는 5,3,1과 무한히 많은 0을 좌표로 갖는다.
우리는 이것을 첫 기저함수에 5를 곱하고 두번째 기저함수에 3을 곱하고 세번째 기저함수에 1을 곱하고
다른 기저함수는 더하지 않는 것으로 보면 된다.

4x^7- 5x^2의 좌표값은 0,0,-5,0,0,0,4 그 뒤론 무한하게 0이다.

일반적으로, 각 다항식은 유한히 많은 항을 가지고 있어서 그 좌표 역시 유한한 수의 수와 무한히 많은 0으로 이루어진다.

이런 좌표 시스템에서 미분은 대부분 0이고 옆 대각선은 양수인 무한 행렬로 표현할 수 있다.
직접 이 행렬을 구해보자

x^3+5x^2+4x+5를 나타내는 좌표를 행렬 오른쪽에 쓴다.
첫번째 좌표에 영향을 주는 항은 1x4밖에 없다.
즉 상수항은 4가 된다.

이는 4x를 미분해서 4가 나온것과 일치한다.
행렬과 벡터의 곱에서 두 번째 좌표는 2x5이다. 이는 미분결과 x의 계수가 10이라는 것을 말한다.

역시 5x^2를 미분한 결과와 일치한다.
마찬가지로 행렬과 벡터의 곱에서 세 번째 항은 3x1이다.
x^3을 미분하면 3x^2가 되는 것과 일치한다.

나머지는 다 0이다.
이것이 가능한 이유는 미분이 선형이기 때문이다.
각 기저함수를 미분한 뒤 각 열에 집어넣으면 행렬을 구할 수 있다

행렬-벡터 곱과 미분은 겉보기엔 완전히 달라보였지만 알고보면 같은 종류이다.
정리하자면,
선형대수에서의 벡터를 화살표로 보고 내적, 고유벡터 같은 대부분의 개념은 함수에서도 사용되는 개념이다.
대신 내적 또는 고유함수처럼 다른 단어를 쓴다.
즉, 수학에서 벡터와 비슷하게 쓰이는 개념들은 매우 많다.
화살표, 숫자 배열, 함수 같이 벡터와 비슷한 것들의 집합을 벡터 공간이라고 한다.
우리는 벡터 공간의 모든 종류에 대해 다루고 싶지 않기 때문에 벡터 합과 실수배에서 파생된 규칙을 정립해야 한다. 이를 공리(Axioms)라고 부른다.

이 공리들은 내가 생각하는 벡터공간과 새로운 벡터공간에 그 이론을 적용하고 싶은 사람을 연결해주는 다리이다.
그래서 다른 사람의 공간에서의 벡터 정의가 이 공리를 만족한다면 다른건 고려하지 않고도 선형대수의 결론을 적용할 수 있다.
다시 말해, 결론을 구체적인 종류의 벡터로 표현하는 것이 아니라 공리들의 관점에서만 보는 것이다.
그래서 Chapter1 에서 수학자들은 벡터를 "합과 실수배가 공리를 만족하게 정의되어 있으면 무엇이든 벡터가 될 수 있다."고 보는 것이다.
즉, 선형대수학은 벡터를 화살표로 보는 것보다 더 광범위하게 적용할 수 있는 것이다.
- 공리?
- 새로운 벡터 공간에서 벡터와 비슷한 것들의 정의를 검증해볼 때 사용하는 일종의 체크리스트
'수학 > 선형대수학' 카테고리의 다른 글
| [3Blue1Brown] Chapter 12 | 크래머 공식의 기하학적 설명 (0) | 2022.08.08 |
|---|---|
| [3Blue1Brown] Chapter 15 | A quick trick for computing eigenvalues (0) | 2022.08.07 |
| [3Blue1Brown] Chapter 14 | Eigenvectors and eigenvalues (0) | 2022.08.07 |
| [3Blue1Brown] Chapter 13 | Change of basis (0) | 2022.08.06 |
| [3Blue1Brown] Chapter 11 | Cross products in the light of linear transformations (0) | 2022.08.04 |
