{학습 목적}
Chapter 14에서는 고유벡터, 고유값, 고유기저에 대해 학습한다.
고유벡터, 고유값, 고유기저를 공부하는 이유는 행렬에서 이 값들을 알아내어 변환이 되지 않는 경우도 있지만
대각선 행렬을 만들어 행렬의 계산을 쉽게 하기 위해서라고 생각한다.
<고유벡터, 고유값>
고유벡터, 고유값을 아는데 중요한 개념은 행렬을 선형변형으로 보는 것, 행렬식, 선형방정식계, 기저변환이다.
이차원 선형변환에 대해 생각해보자
이 변환은 기저 벡터인 i-hat을 좌표 [3,0]으로, j-hat을 [1,2]로 옮겨서 열이 [3,0]과 [1,2]인 행렬로 나타난다.

한 특정한 벡터의 변환과 벡터의 종점과 시점을 지나는 선인 그 벡터의 스팬에 대해서 생각해보자.
대부분의 벡터는 변환의 과정에서 자신의 스팬을 벗어날 것이다.

만약, 벡터가 변환 후 위치하는 장소가 자신의 스팬 어딘가가 된다면 상당히 우연처럼 보일 것이다.
하지만 몇몇 특별한 벡터들은 고유한 스팬에 남아있다.
이것은 행렬이 이러한 벡터들을 마치 스칼라인 것처럼 늘이고 줄이는 것 밖에 하지 않는다는 뜻이다.
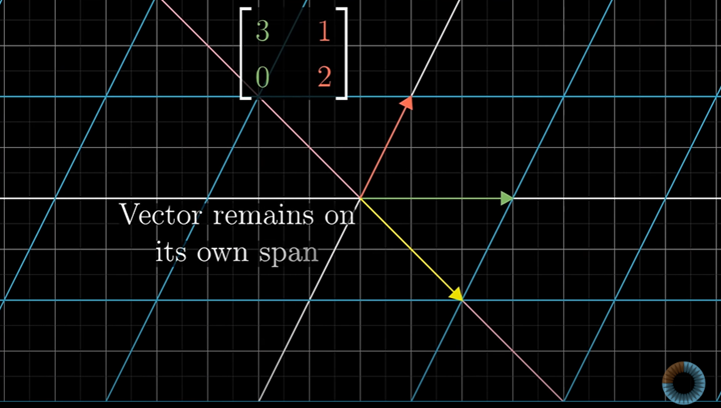
즉 기저 벡터인 i - hat은 특별한 벡터로 볼 수 있다. i-hat의 스팬은 x축이고, 행렬의 첫 열에서 나온 것이다.

우리는 i-hat이 자신의 3배가 되게 움직여도 x축 위에 있는 것을 볼 수 있다.

또 변환의 선형성 때문에 x축 위의 다른 벡터도 3배로 늘어나고 자신의 스팬에 남아있다.

이 변환 과정에 스팬이 변하지 않는 또 다른 벡터는 바로 [-1,1]이다.
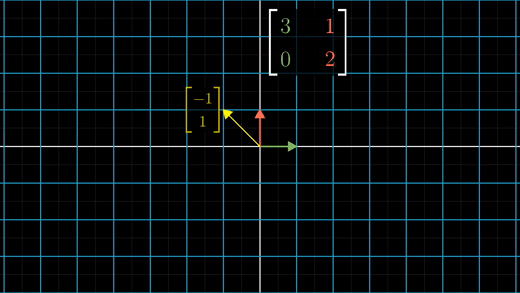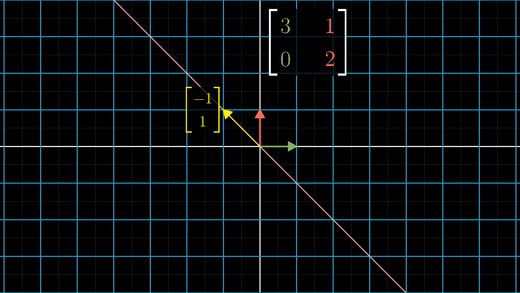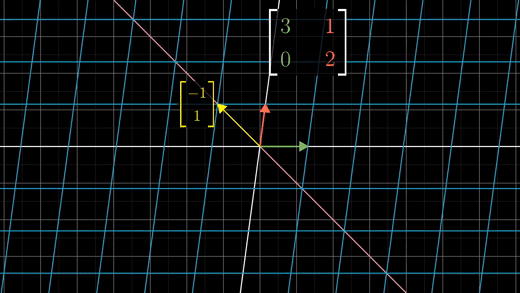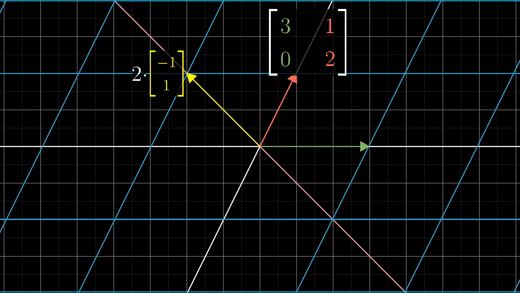
이 벡터는 두 배로 늘어나게 된다.
그리고 선형성에 의해 이 대각선 위에 있는 다른 벡터도 2배로 늘어나게 될 것이라는 것을 알 수 있다.

이 변형에서 이것들은 변환 후에도 스팬을 유지하는 특별한 성질을 가진 모든 벡터이다.
X축 상의 벡터들은 세 배로 늘어나고 대각선 상의 벡터들은 두 배로 늘어난다.

변환 도중에 고유벡터를 제외한 벡터들은 회전이 되어 스팬하는 선 위를 벗어날 것이다.

즉, 이러한 특별한 벡터들을 “고유벡터(eigenvectors)”라고 부른다.
그리고 각 고유벡터들은 “고유값(eigenvalue)”이라고 불리는 값들을 가지고 있다.
이것은 변환 도중 늘어나고 줄어드는 배수이다.

고유값 -1/2를 가진 고유벡터를 생각해보자.
이는 벡터가 음의 부호로 인해 뒤집어지고 1/2 만큼 줄어든다는 것을 의미한다.

여기서 중요한 것은 벡터가 스팬하는 선 위에 머무르고 회전해서 벗어나는 일이 없다는 것이다.
삼차원 회전을 생각해보자.
만약 이 회전에서의 고유 벡터, 자신의 스팬에 남아있는 벡터를 찾을 수 있다면 그것이 바로 회전축이다.

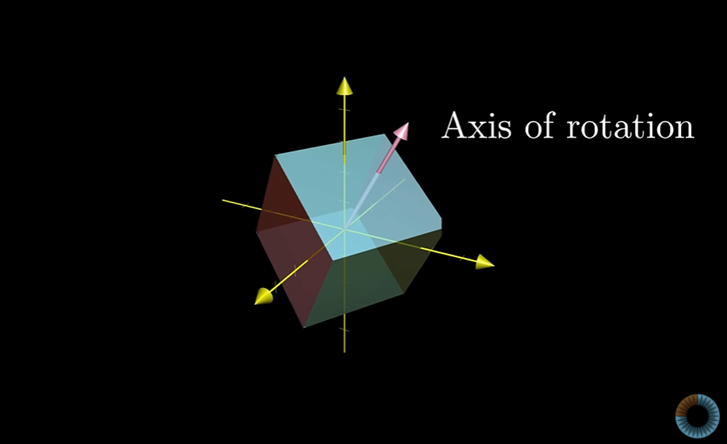
그리고 3D회전을 생각할 때는 몇 개의 회전축(고유 벡터)과 회전하게 되는 각을 가지고 생각하는 것이 훨씬 편하다.
이 변환과 관련된 3x3 행렬 전체를 생각하는 것보다 말이다.

이 경우에는 회전이 그 무엇도 늘이거나 줄이지 않으니 고유값은 1이 될 것이다.
회전 후에도 벡터의 길이가 변하지 않는다는 것이다.

이 경우에는 회전이 그 무엇도 늘이거나 줄이지 않으니 고유값은 1이 될 것이다.
이 유형은 행렬로 묘사된 선형변환에서 많이 등장한다.
이 행렬의 열을 기저 벡터의 위치로 읽어 내릴 수 있다면 변환 후 무엇이 일어나는지 알 수 있다.
하지만 선형변환 중 일어나는 일에 대해 확실하게 느낌을 받으려면 고유벡터와 고유값을 찾아야한다.

상징적으로 고유의 벡터의 개념은 이런 형식이다.

A는 임의의 변환을 나타내는 행렬이며, v는 고유벡터, λ는 고유값인 상수이다.
이 표현이 나타내는 것은 행렬-벡터 곱셈인 Av가 고유벡터 v를 임의의 상수 λ로 스케일링 한 결과와 같다는 것이다.

따라서 행렬 A의 고유벡터와 고유값을 찾는 것은 이 표현을 참으로 만드는 v와 λ값을 찾는 것이 된다.
왼쪽이 행렬-벡터 곱셈인 반면에 오른쪽은 스칼라-벡터 곱셈이여서 계산하기가 어렵다.
오른쪽을 임의의 벡터를 λ배로 스케일링 하는 행렬-벡터 곱으로 쓰는 것부터 시작해보자

이러한 행렬의 열은 각 기저 벡터의 일어나는 변화를 나타내는데 여기선 단순히 λ배를 하므로
이 행렬은 단순히 대각선 아래로 상수 λ를 가지고 다른 곳은 전부 0이 들어간다.

좀 더 보편적인 방법은 λ를 묶어내서 λI로 쓰는 것이다. (I는 대각선에 1이 있는 항등행렬)

양변이 모두 행렬-벡터의 곱으로 나타내졌으니 양변을 빼서 v라는 인수로 묶어낼 수 있다.
이제 새로운 행렬 A-λI를 얻었으니 이 행렬과 곱해서 영벡터를 만드는 벡터 v를 찾아야 한다.
이 때, 벡터 v가 영이 아닌 벡터를 찾아보자.

영벡터가 아닌 벡터와 행렬을 곱해서 0이 되게 만드는 방법은 행렬에 일어나는 변환이 차원을 낮은 차원으로 내리는 것이면 된다.

이 축소는 행렬이 0 행렬식이 되게 한다.

예를 들어, 어떤 행렬 A가 [2,1]과 [2,3]이라는 열을 가지고 변수 λ를 각 대각선의 값에서 빼는 경우를 생각해보자
이제 λ의 값이 바뀐다고 생각해보자.
λ의 값이 바뀌면, 행렬이 바뀌고 행렬식도 바뀌게 된다. 이 행렬식을 0으로 만드는 λ값을 찾는 것은 이 공간의 차원을 낮추는 변환을 찾는 것이다.

이 경우에는 λ = 1이 된다.

이것이 갖는 의미를 해석해보자.
λ=1일 때, 행렬 A-λI는 선이 된다. (A-λI)*v를 영벡터로 만드는 영벡터가 아닌 v벡터가 있다는 것이다.

지금 우리가 이걸 하고 있는 것은 Av =λv로 만드는 v벡터가 변환 A에서 스팬이 변하지 않는 고유벡터 v이기 때문에
이 벡터를 찾고있는 것을 기억해야한다!
이제까지의 개념을 정리해서 다시 예시를 살펴보자
[3,0]과 [1,2]의 열을 가지는 행렬과 고유값이 되는 λ의 값을 찾기 위해 이 행렬의 대각선에서 빼서 행렬식을 계산한다.이렇게 하면 λ에 대한 이차식인 (3-λ)(2-λ)를 얻는다.

이 때 가능한 고유값은 λ=2, λ=3 밖에 없다는 결론을 얻는다.
이 중 하나의 고유값을 가지는 고유벡터를 알아내기 위해 λ=2라고 가정하자.
λ의 값을 행렬에 집어 넣어서 대각선이 바뀐 이 행렬이 [2,0]을 어떻게 변환하는지 보자

이걸 계산하면 해가 [-1,1]이 스팬하는 대각선 위에 있는 모든 벡터라는 사실을 알 수 있다. (고유벡터)

이건 원래 행렬 3,0,1,2 가 이 벡터들(고유벡터)을 두 배로 늘린다는 사실과 일치한다. (Av = λv니까)

2d 변환은 고유벡터가 무조건 존재하지 않는다.
예를 들어, 고유벡터가 없는 90도 회전의 경우에는 모든 벡터가 자신의 스팬을 벗어난다.

이러한 회전변환에서 고유벡터를 구하면 어떤 일이 일어날까?
행렬의 열이 [0,1]과 [-1,0]이고 대각선 성분에서 λ를 빼고 행렬식이 0이 되는 경우를 찾아보면
다항식 λ^2+1을 얻게 되어 이 다항식의 해는 허수 i와 -i뿐이다.

실수해가 없다는 것은 고유벡터가 없다는 것이다.
미는 변환에 대해서도 생각해보자
i-hat은 그대로 두고 j-hat은 1만큼 움직이면 행렬의 열이 [1,0]과 [1,1]이 된다.
x축 위에 있는 모든 벡터들은 그 자리에 그대로 있기 때문에 i-hat은 고유값 1을 가지는 고유벡터가 된다.
즉, 이 벡터들은 대각선에서 λ를 빼고 행렬식을 계산했을 때 얻는 유일한 고유벡터이다.
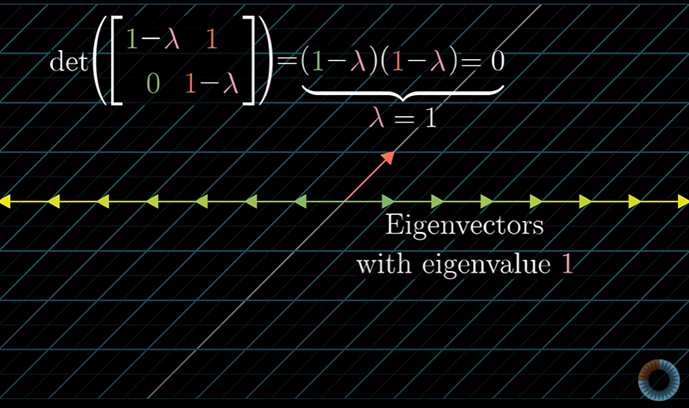
하나의 고유값을 가지면서도 다양한 고유벡터를 가질 수 있는 경우도 있다.
간단한 예는 모든 것을 두 배로 스케일 하는 행렬인데, 고유값은 2이지만 평면상의 모든 벡터는 고유벡터가 된다.

마지막으로 "고유기저(eigenbasis)"에 대해 알아보자
예를 들어 기저벡터들이 고유벡터인 경우를 보자.

i-hat은 1만큼, j-hat은 2만큼 스케일 되었다고 하자
새로운 좌표로 행렬의 열을 써내면 i-hat과 j-hat의 고유값인 스칼라 곱 -1과 2가 행렬의 대각선에 있고 다른값들은 모두 0이다.

이를 "대각선 행렬(diagonal matrix)"이라고 한다.
이를 해석하면, 모든 기저벡터는 고유벡터이고 대각선의 값들은 고유값이 된다.

대각선 행렬이 다루기 좋은 이유 중 하나는 만약 이 행렬을 아주 많이 곱한다면 무엇이 일어날지 계산하기 쉽다는 것이다.

이 행렬이 하는 것은 각 기저벡터를 특정한 고유값으로 스케일하는 것이기 때문이다.
이 행렬을 100번 정도 적용하는 것은 기저벡터(=고유벡터)들을 고유값의 100의 제곱으로 스케일링 하는 것과 동일하다.
하지만 만약 변환이 고유벡터들을 많이 가지고 있다면 고유벡터가 기저벡터가 되도록 좌표계를 바꿀 수 있다.

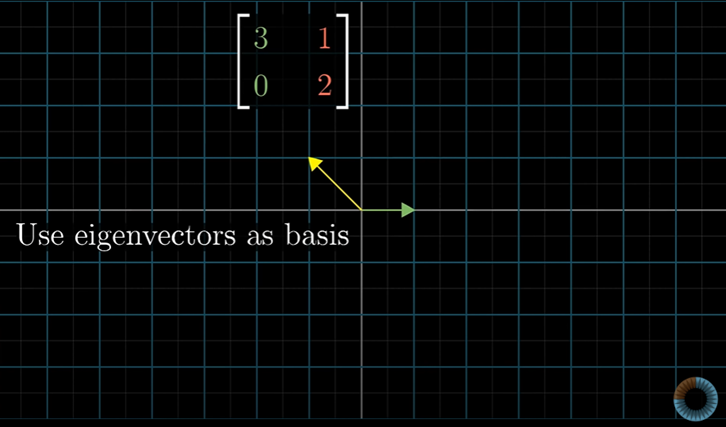
새로운 기저로 쓰고 싶은 벡터의 좌표를 가져와 (현재 좌표계에서는 두 고유벡터가 된다) 행렬의 열을 구성한다.
이것이 기저행렬을 바꾸는 것이다.

바뀐 기저행렬을 오른쪽에 두고 왼쪽에 바뀐 기저 행렬의 역을 두고 원래 변환을 사이에 끼면 같은 변환을 나타내지만 다른기저 벡터 좌표계를 쓰는 행렬을 얻는다.


이걸 고유벡터로 하는 이유는 새로운 행렬이 대각선에 고유값을 가지는 대각선 행렬이 되게 하기 위해서이다.

기저벡터이기도 한 고유벡터의 쌍은 고유기저라고 부른다.
만약 이 행렬의 100 제곱을 계산해야한다면 고유기저로 바꾼 후 100제곱을 계산하고 다시 원래의 계로 전환하는 것이 훨씬 쉬울 것이다.
이 변환이 모든 변환에서 되는 것이 아니다.
미는 변환은 변환 후 모든 공간을 스팬하는 고유벡터가 없기 때문이다.
하지만 고유기저를 찾을 수 있다면 행렬 계산이 매우 쉬워진다.
- 고유벡터
- 변환 후 벡터의 장소가 그 벡터의 스팬 위에 있는 벡터
- 고유값
- 고유벡터의 스케일링 인자
- 고유기저
- 기저벡터이면서 고유벡터가 되는 벡터들
'수학 > 선형대수학' 카테고리의 다른 글
| [3Blue1Brown] Chapter 16 | Abstract vector spaces (0) | 2022.08.07 |
|---|---|
| [3Blue1Brown] Chapter 15 | A quick trick for computing eigenvalues (0) | 2022.08.07 |
| [3Blue1Brown] Chapter 13 | Change of basis (0) | 2022.08.06 |
| [3Blue1Brown] Chapter 11 | Cross products in the light of linear transformations (0) | 2022.08.04 |
| [3Blue1Brown] Chapter 10 | Cross products (0) | 2022.08.03 |
