{학습 목적}
Chapter 12 에서는 크래머 공식을 기하학적으로 설명하고 있다. 이 부분을 학습하는 이유는 단순히 크래머 공식을 적용하여 미지 벡터의 좌표를 구하는 것을 배우는 것이 아닌 행렬식과 선형방정식계의 관련성에 대해 깊게 이해해보기 위한 것이라고 생각한다.
<크라메르 공식의 기하적 설명>
두 개의 미지수x,y와 그에 대한 방정식 두 개로 이루어진 선형연립방정식이 있다고 하자

이 방정식을 기하학적으로 생각할 수 있다.
어떤 미지 벡터 [x,y]가 주어진 행렬에 의해 선형 변환 되면 그 결과값은 식에서 주어진 [-4,-2]가된다.
이 행렬의 열은 벡터가 변환시 어떻게 변해가는가를 알려준다.
즉 각 열은 변환 전 공간의 기저 벡터가 변환 후 도달하는 곳을 알려주는 것이다.
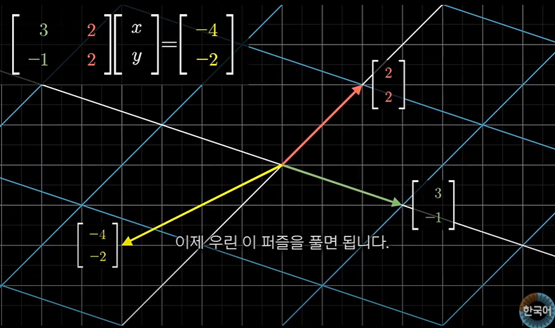
어떤 입력값 [x,y]가 결괏값인 [-4,-2]에 도달할 수 있을까?
이 질문에 답하기 위해 먼저 주어진 결과 벡터가 행렬들의 열들의 선형 결합임을 알아야한다.
결과 벡터는 x[i-hat의 변환] + y[j-hat의 변환]과 같다.

우선적으로, 얻어질 답의 형태는 변환 후 선형공간이 하위차원으로 줄어드느냐 않느냐로 결정된다.
즉 행렬식이 0인지 여부를 확인하는 것이다.
행렬식이 0인 경우, 입력값이 모두 주어진 결과값에 도달하지 못하고

저 결과값에는 모든 입력값이 다다를 수 있다.

이 강의에서는 행렬식이 0이 아닌 벡터쌍의 경우만 다룰 것이다.
이 변환의 결과 벡터는 여전히 변환 전처럼 n차원의 공간을 생성할 수 있다.
즉 모든 입력값에 딱 한 결과값이, 모든 결과값에는 한 입력값이 대응한다.
첫 번째로 방법을 옳지 않지만 옳은 방향의 접근법을 보여준다.
이 미지 입력벡터의 x좌표는 첫 번째 기저벡터 [1,0]과의 내적으로 얻을 수 있다.
마찬가지로 y좌표는 두 번째 기저 벡터 [0,1]과의 내적으로 얻을 수 있다.

변환 후에 기저 벡터가 변환되어 만들어진 미지 벡터와 변환 벡터의 내적 역시 이러한 x좌표, y좌표가 있을 것이다.

이렇게 하면 우리는 벡터가 어떤 선형결합으로 이루어질지 알게된다.
하지만 이는 참이 아니다.
대부분의 벡터들에 대해 선형변환 이전과 이후의 내적은 매우 다르다.
단적인 예로, 두 벡터가 모두 같은 방향, 양의 방향을 가리키고 그 내적이 양의 실수일 때
변환 중에 서로 멀리 떨어지게 되면 그 결과 둘의 내적이 음의 실수가 된다.
마찬가지로 시작 벡터가 수직인 관계라서 내적이 0 일 때, 즉 기저벡터 같은 경우
그들이 변환 이후에 수직으로 남아있을 거란 보장이 없다.
둘의 내적이 0으로 보존되리라는 보장이 없다는 것이다.
내적이 보존되는 변환은 상당히 특수한 경우이다.
이 경우를 직교변환(orthonormal transformations)라고 부른다.

이들은 기저 벡터의 수직 상태, 길이까지도 유지되는 변환이다.
다시 말해 고정된 움직임에 대응하는, 늘거나 줄거나 등의 변형이 없는 회전변환행렬로 생각할 수 있다.
직교 행렬의 선형 방정식은 매우 쉽게 풀린다.
이 변환에서는 내적이 보존되기 때문에 결과 벡터와 행렬의 모든 열의 내적은 구하려는 벡터와 모든 기저벡터 사이의 내적과 같다.
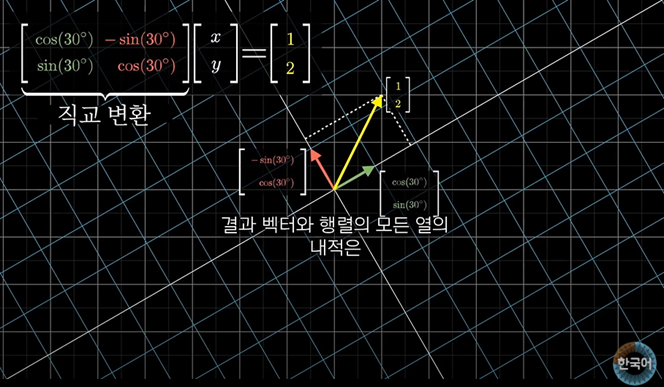

즉 입력벡터의 좌표를 바로 찾을 수 있을 것이다.
그래서 이러한 매우 특수한 경우에서는 x는 첫째 열과 결과 벡터의 내적이 될 것이고
y는 둘째 열과 결과 벡터의 내적이 될 것이다.
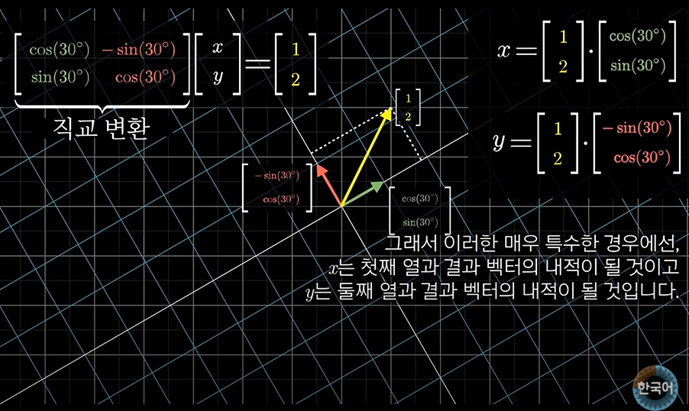
그렇다면 변환 후에도 입력벡터에서 변하지 않고 남아있는 다른 기하학적인 무언가는 없을까?
여기서 행렬식의 아이디어가 사용된다.
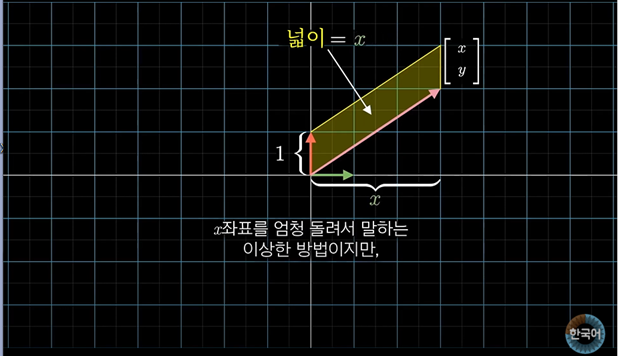
첫 번째 기저 벡터 i-hat과 미지수 벡터 [x,y]를 가지고 평행사변형을 그린다.
이 평행사변형의 넓이는 밑변 1과 y좌표의 곱으로 구할 수 있다.

다시 말해, 평행사변형의 넓이는 벡터의 y좌표를 돌려 설명하는 다소 난해한 방법이다. 저 넓이에는 부호가 존재한다.
이 말은 즉슨 벡터의 y좌표가 음수일 때, 평행사변형의 넓이도 음수가된다.
[x,y]벡터와 두번째 기저벡터인 j-hat으로 생성되는 평행사변형은 그 넓이가 x좌표인 것이다.
이것이 일반화된 사례로 3차원을 보자.
z좌표를 뽑아내고자 한다면, [x,y,z]벡터와 기저 벡터 k-hat의 내적을 취하면 된다.
하지만 아까 보았던 기하적 대안을 가지고 좌표를 생각한다면 k-hat을 제외한 i-hat , j-hat으로 생성되는 평행육면체를 생각해볼 수 있다.
밑면이 i-hat, j-hat으로 생성되는 정사각형으로서 넓이가 1이기에 평행육면체의 부피는 그 높이와 같을 텐데 그것이 바로 벡터의 z좌표이다.
즉, 3차원에서는 찾으려는 좌표를 제외한 다른 기저 벡터 두 개와 미지 벡터로 생성되는 평행육면체의 부피를 찾으면 그 부피가 그 벡터의 좌표가 된다.
또한 오른손법칙을 이용해서 부피에 부호가 있다고 생각한다. 오른손 법칙을 이용해서 말이다.
즉 벡터의 세 순서가 중요하다는 것이다.
그렇게 하면 음의 좌표들도 여전히 부피로서 성립한다.
그래서 왜 어렵게 좌표들을 넓이나 부피의 관점으로 보고 있을까?
행렬변환을 적용했을 때, 평행사변형의 넓이는 유지되지 않고 더욱 커지거나 줄어들게 된다.
이제 여기서 행렬식의 핵심 발상을 이용한다(!)
모든 넓이는 변환 행렬의 행렬식 배 만큼 일정한 양으로 증가하게 된다.

예를 들어, 첫 번째 기저벡터 (= 행렬의 첫번째 열)과 변환된 미지 벡터[x,y]로 생성된 평행사변형에 대해 그 넓이는 얼마일까?
원래 평행사변형 넓이가 미지 벡터의 y좌표였으니,

변환 후 넓이는 (변환의 행렬식 )x (y좌표) 값이 될 것이다.
따라서 y가 구해질 수 있게 된다.

y는 결과값의 (변환 후 평행사변형의 넓이)를 (전체변환의 행렬식)으로 나눈 값이다.

넓이를 구하는 방법은 우리는 미지의 벡터가 어디에 도달하는 지 알기 때문에 그것이 선형 연립방정식의 전체 핵심이다.
새 행렬을 만들어서 첫 번째 열은 원래 행렬과 똑같이 넣고
두 번째 열에는 결과 벡터를 넣은 다음 그 행렬식을 구하는 것이다.
변환 후 행렬의 열과 벡터의 좌표들만 가지고 미지벡터 y좌표를 복구할 수 있다.

같은 발상을 x좌표에도 적용할 수 있다.

이 평행사변형의 변환된 형태는 결과 벡터와 행렬의 두 번째 열로 생성되고 변환 후 넓이는 (변환의 행렬식) x (원래 넓이)이다.

따라서 x좌표는 변환 후의 넓이/변환의 행렬식으로 구할 수 있다.
전에 한 것과 비슷하게, 평행사변형의 넓이는 첫 번째 열에는 결과 벡터를 넣고
두 번째 열에는 원래 행렬의 열을 넣은 새로운 행렬을 만들어 구할 수 있다.
이렇게 다시 선형방정식의 결과값들의 정보들만을 가지고 x를 구할 수 있다.

이렇게 선형방정식의 해를 구하는 이 공식을 크라메르 공식이라고 한다.
'수학 > 선형대수학' 카테고리의 다른 글
| [3Blue1Brown] Chapter 16 | Abstract vector spaces (0) | 2022.08.07 |
|---|---|
| [3Blue1Brown] Chapter 15 | A quick trick for computing eigenvalues (0) | 2022.08.07 |
| [3Blue1Brown] Chapter 14 | Eigenvectors and eigenvalues (0) | 2022.08.07 |
| [3Blue1Brown] Chapter 13 | Change of basis (0) | 2022.08.06 |
| [3Blue1Brown] Chapter 11 | Cross products in the light of linear transformations (0) | 2022.08.04 |
