{학습 목적}
Chapter 2에서는 기저, 선형조합, 스팬에 대한 개념을 학습한다.
이 개념을 학습하는 이유는 기저, 선형조합, 스팬은 벡터를 통한 공간의 형성이라는 컨셉에 대한 기본적인 구성요소이기 때문이라고 생각한다.
즉, 기저를 선형조합함으로써 어떠한 span(확장공간)을 만든다는 것을 이해할 수 있다.
<선형조합, 스팬, 기저>
[기저]
단위 벡터(unit vector):
x축의 단위 벡터 - 오른쪽 방향의 길이 1 벡터, 'i-hat'
y축의 단위 벡터 - 왼쪽 방향으로 길이 1 벡터, 'j-hat'
i-hat, j-hat를 좌표의 기저(basis)라고 부른다.
즉, 좌표값을 스칼라로 생각해보면, 기저 벡터들은 그 스칼라(좌표값)가 스케일링 하는 대상이 된다.
[선형조합]
좀 더 기술적인 정의로 보자면, 좌표계를 이 두 개의 특별한 기저 벡터로 구성(framing)하는 것이다.
스칼라(좌표값)을 이용해 각 기저 벡터 하나를 스케일링 하고, 두 스케일링 된 더하는 방법으로 좌표계에 있는 벡터들을 표현할 수 있다. 이 방법을 벡터의 선형 조합이라고 부른다.
벡터의 선형 조합(linear combination):
두 벡터를 스케일링하고 나서 더하는 것

[스팬]
Span(확장공간): 주어진 두 벡터 쌍의 조합으로 나타날 수 있는 결과 벡터들의 집합
선, 평면에 대해서 모든 2차원 벡터를 떠올릴 때, 각 벡터의 끝이 가르키는 점들로 개념화 하면 좋다.
그럼 결과적으로 무한하고 평평한 2차원 평면 그 자체를 떠올리는 것과 같아진다.
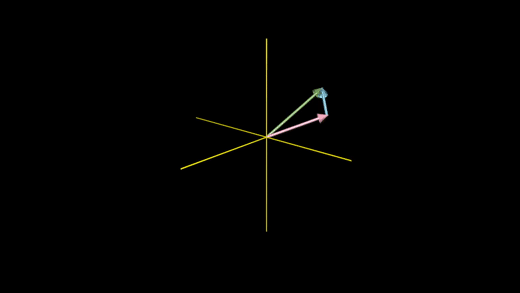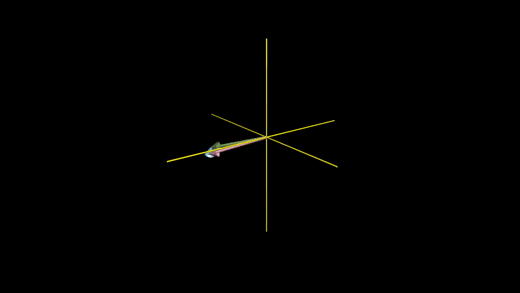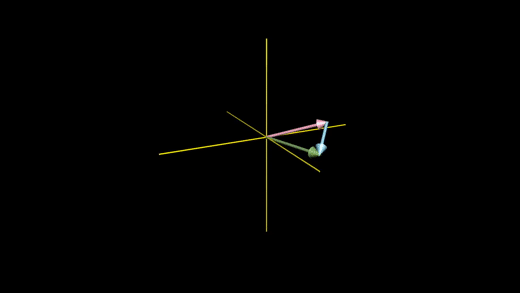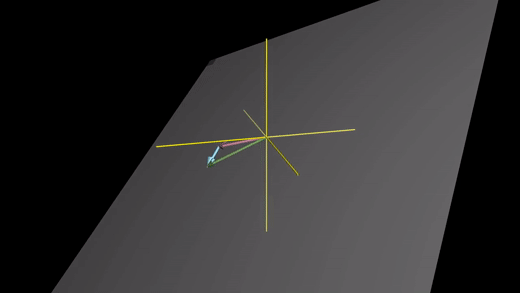
스팬과 같은 개념을 3차원 공간에서 생각해본다면, 스칼라들로 두 스케일링 된 벡터의 합에 영향을 주고, 따라서 결과 벡터의 끝에도 영향을 준다. 그 끝은 3차원 공간의 원점을 가로지르는 평평한 공간이 될 것이다. 이 평면이 두 벡터의 스펜(span,확장공간)이다.
좀 더 정확하게 말하자면, 평면 위에 끝을 놓는 모든 벡터들의 집합이 두 벡터의 스펜이다.
선형 종속(linear dependent): 스팬의 축소 없이 하나 이상의 벡터를 제외시켜도 되는 경우, 벡터들 중 하나가 다른 벡터들의 선형 조합으로 표현 가능한 경우 , 이미 다른 벡터의 스팬에 포함되는 경우
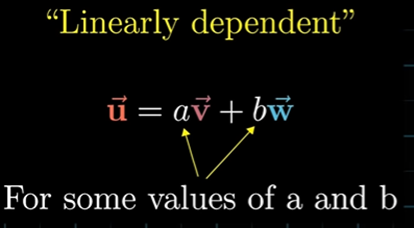
ex) 세 번째로 추가한 벡터가 다른 두 벡터가 만드는 스팬인 평면에 놓여 있을 때
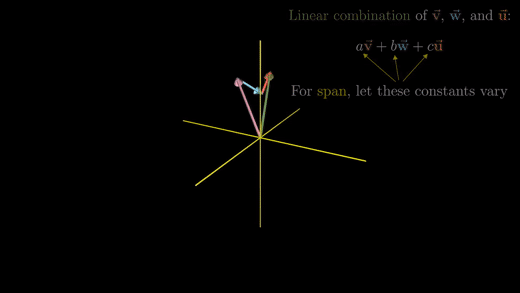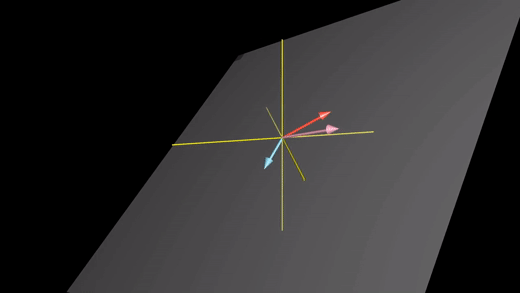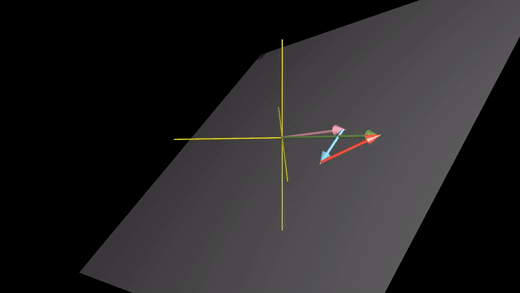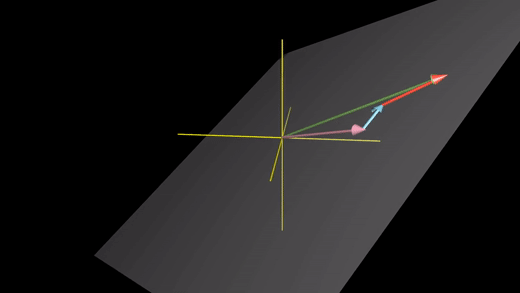
선형 독립(linear independent): 각각의 벡터가 기존 스팬에 또 다른 차원을 추가하는 게 가능한 경우
ex) 세 번째 벡터가 두 벡터의 스팬인 평면 위에 있지 않을 때, 3차원의 모든 벡터들에 대한 접근이 가능해짐.
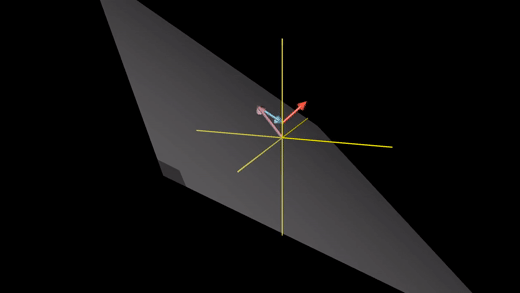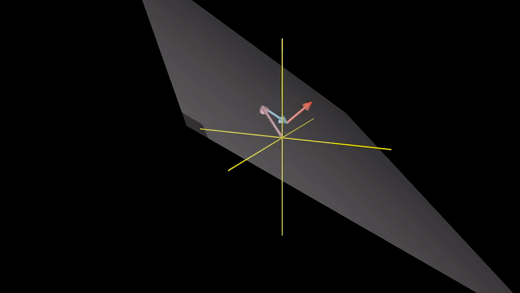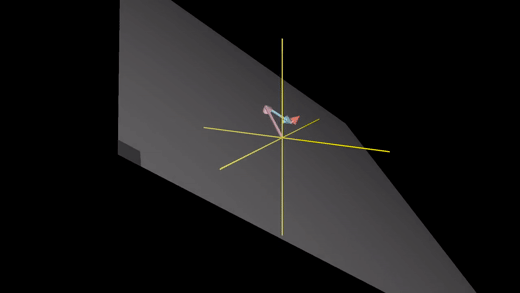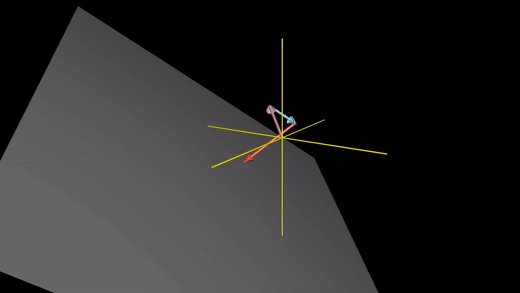
- 기저?
- 좌표계를 이루는 근본 벡터
- 선형조합?
- 길이를 늘이거나 줄이거나 방향을 바꾼 기저 벡터들끼리의 합
- 스팬?
- 선형조합으로 나타나는 결과 벡터들의 집합, 즉, 스팬은 점, 선, 공간이 될 수 있다.
'수학 > 선형대수학' 카테고리의 다른 글
| [3Blue1Brown] Chapter 6 | The determinant (0) | 2022.07.30 |
|---|---|
| [3Blue1Brown]Chapter 5 | Three-dimensional linear transformations (0) | 2022.07.29 |
| [3Blue1Brown]Chapter 4 | Matrix multiplication as composition (0) | 2022.07.29 |
| [3Blue1Brown] Chapter 3 | Linear transformations and matrices (0) | 2022.07.29 |
| [3Blue1Brown] Chapter 1 | Vectors (0) | 2022.07.29 |
